Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 43
Para levantar o mastro , uma armação leve é presa ao mastro e uma força trativa de é aplicada ao cabo de sustentação pelo guincho em . Calcule o momento desta força trativa em relação à dobradiça no ponto .
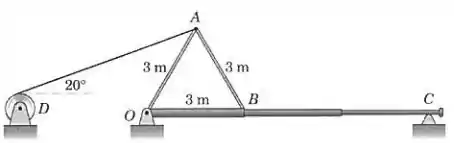
Passo 1
A distância da linha de ação da força de até o ponto é representada em vermelho na figura a seguir:
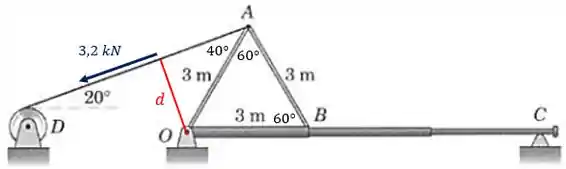
Assim, pela geometria dos triângulos, temos:
Logo, o momento da força em relação a , no sentido anti-horário (positivo), será dado por:
Resposta
(sentido anti-horário)
Exercícios de Livros Relacionados
A região do pé está sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.
A força de 70N age no final do tubo B . Determine ( a ) o momento dessa força em relação ao ponto A e ( b ) a intensidade e a direção de uma força horizontal, aplicada em C , que produz o mesmo moment
A lança do elevador é estendida até a posição mostrada. Se o operário pesa 800N ( ≈ 80k g ) , determine o momento dessa força em relação à conexão em A .
Sabe-se que é necessária uma força com um momento de 960 N ⋅ m em relação a D para endireitar o mourão CD. Se d=2,8 m, determine a tração que deve ser desenvolvida no cabo do guincho A B para criar o
A força de 300 N é aplicada em A como mostrado na figura. Determine (a) o momento da força de 300 N sobre D, (b) a menor força aplicada em B que cria o mesmo momento em D.