Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 1

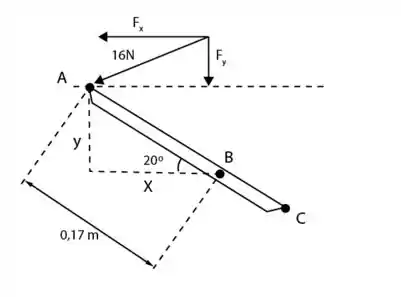
Uma válvula de pedal para um sistema pneumático é articulada em B. Sabendo que α = 28 º , determine o momento de uma força de 16 N em relação ao ponto B decompondo a força em componentes horizontal e vertical.

Passo 1

Desenhando o diagrama do corpo livre:

Passo 2

Do diagrama do corpo livre, pode-se escrever:

θ = α - 20 º = 28 - 20 = 8 º

Decompondo F obtemos:

F x = 16 ⋅ cos ⁡ 8 º =   15,844 3   N F y = 16 ⋅ s e n 8 º = 2,226 8   N

Encontrando as distâncias x e y   :

x = 0,17   m × cos ⁡ 20 º = 0,159 748   m y = 0,17   m × sen ⁡ 20 º = 0,058 143   m

Passo 3

Podemos calcular, por fim o momento MB:

M B = y F x + x F y M B = 0,058 143 ⋅ 15,8443 + 0,159 748 ⋅ 2,2268 M B = 1,277   N ⋅ m     ( m o m e n t o   n o   s e n t i d o   a n t i - h o r á r i o )

Passo 4

Podem-se calcular as componentes da força na direção x ,   y   e o momento em relação ao ponto B:

F x = 15,844 3     N F y = 2,226 6   N M B = 1,277   N ⋅ m  

Resposta

M B = 1,277   N ⋅ m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cabo do martelo está sujeito à força F = 100N . Determine o momento dessa força em relação ao ponto A .
Para arrancar o prego em B , a força F exercida sobre o cabo do martelo precisa produzir um momento no sentido horário de 60N ∙ m em relação ao ponto A . Determine a intensidade necessária da força F
Dados os três vetores não nulos A , B e C , mostre que se A ∙ B × C = 0 , os três vetores necessitam estar no mesmo plano.
Se o momento produzido pela força de 4k N em relação ao ponto A é 10k N . m no sentido horário, determine o ângulo θ , onde 0 ° ≤ θ ≤ 90 ° .
Se A , B e D são vetores, prove a propriedade distributiva para o produto vetorial, ou seja, A × B + D = A × B + ( A × D ) .