Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 30

A viga é composta por três peças de plástico coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a força de cisalhamento vertical à qual resiste a aba superior da viga. Os apoios em C e D exercem somente reações verticais sobre a viga

Passo 1

Vamos calcular as reações de apoio.

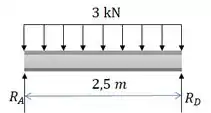
Como a carga e as reações são simétricas

R A = R B

Aplicando o somatório de forças verticais

∑ F y = 0 ⇒ R A - 3 ⋅ 2,5 ⋅ R B = 0

R A = R B = 3,75   k N

Passo 2

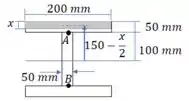
Agora vamos calcular o momento de inércia:

I = 200 ⋅ 300 3 12 - 200 ⋅ 200 3 12 + 50 ⋅ 200 3 12

I = 350 ⋅ 10 6   m m 4

Passo 3

Para calcular a força sobre uma aba, primeiro precisamos definir uma função para o momento estático nesta aba.

Q x = 200 ⋅ x 150 - x 2

Q x = 30000 x - 100 x 2

Passo 4

Bem, sabemos por definição que tensão é força sobre área. Em termos infinitesimais:

τ = d F d A

Sabemos que a tensão de cisalhamento é dada por:

V Q ( x )   I t = d F d A

Isolando d F :

d F = V Q ( x )   I t d A

Perceba que a área da seção é quadrada. Em outras palavras: d A = t ⋅ d x

Substituindo o valor de Q ( x ) temos:

d F = V ⋅ ( 30000 x - 100 x 2 )   I t t ⋅ d x

Simplificando:

d F = V I ( 30000 x - 100 x 2 )   ⋅ d x

Integrando

F = V I ∫ 0 50 ( 30000 x - 100 x 2 )   ⋅ d x

F = V I ⋅ 30000 x 2 2 - 100 x 3 3 0 50

Substituíndo os valores:

F = 3,75   k N 350 ⋅ 10 6   m m 4 ⋅ 30000 ⋅ ( 50 m m ) 2 2 - 100 ⋅ ( 50   m m ) 3 3

F = 357,14   N

Resposta

F = 0 , 35714   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga tem seção transversal retangular e é feita de madeira com tensão de cisalhamento admissível τ a d m = 11,2 MPa. Se for submetida a um cisalhamento V = 20 kN, determine a menor dimensão a de sua
A viga tem seção transversal retangular e é feita de madeira. Se for submetida a um cisalhamento de V = 20 kN, e a = 250 mm, determine a tensão de cisalhamento máxima e trace uma curva da variação da
Se a viga de abas largas for submetida a um cisalhamento V = 125 kN, determine a força de cisalhamento à qual a alma da viga resistirá.
A viga está sujeita ao carregamento mostrado na figura, onde P = 7 k N . Determine a tensão de cisalhamento média desenvolvida nos pregos no interior da região AB da viga. Os pregos estão localizados
A escora é construída com três peças de plástico coladas como mostra a figura. Se a carga distribuída w = 3 k N m , determine o fluxo de cisalhamento a qual cada junta colada deve resistir