Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 28
Determine a tensão de cisalhamento máxima que age na seção crítica da viga de fibra de vidro.
Passo 1
Fala! Queremos a tensão máxima. Então a gente precisa achar onde o cisalhamento é máximo.
Vamos começar calculando as reações de apoio:
Aplicando as equações de equilíbrio:
Passo 2
Utilizamos o método das áreas para gerar o diagrama de esforço cortante.
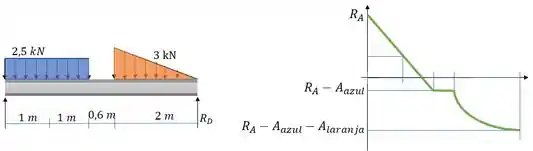
Repara que a gente sobe e desce linearmente até , isso porque temos um carregamento distribuído com constante.
Como não há carregamento até o começo da carga distribuída seguinte, ficamos constantes. Depois, a gente desce o valor total dessa carga triangular, mas repara que a gente o faz em forma de parábola, porque o do carregamento não é constante como o anterior.
E por fim, subimos , chegando em zero.
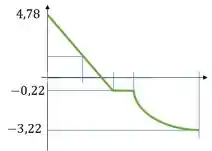
Pelo gráfico, a força cortante máxima é
Com o cisalhamento máximo, gente acha a tensão máxima pela fórmulinha de tensão cisalhante. Bora!
Passo 3
Agora vamos determinar o momento de inércia:
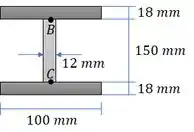
Passo 4
Agora vamos calcular o momento estático. Queremos a tensão máxima, então precisamos do momento estático máximo. Ele ocorre na linha que passa pelo centroide da seção. Como nossa seção é simétrica, calculamos o em relação a metade da seção.
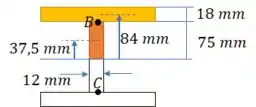
Passo 5
Agora aplicamos a equação do cisalhamento:
Diferente do gabarito, mas está certinho 😉