Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 29
A viga é composta por três peças de plástico coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a tensão de cisalhamento desenvolvida nas juntas coladas na seção crítica. Os apoios em C e D exercem somente reações verticais sobre a viga
Passo 1
Vamos calcular as reações de apoio.
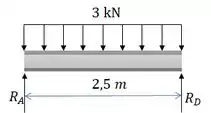
Como a carga e as reações são simétricas
Aplicando o somatório de forças verticais
Passo 2
Agora vamos calcular o momento de inércia:
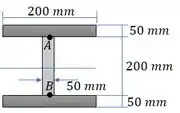
Passo 3
Calculamos o momento estático na aba superior. Por simetria, o momento estático em A e B são iguais. Por consequência, a tensão nestes dois pontos também é igual
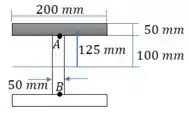
Passo 4
Finalizamos aplicando a equação do cisalhamento:
Resposta
Exercícios de Livros Relacionados
A escora é construída com três peças de plástico coladas como mostra a figura. Se a tensão de cisalhamento admissível para o plástico for τ a d m = 5,6M P a e cada junta colada puder resistir a 50k N
A viga é composta por quatro tábuas pregadas. Se os pregos estiverem de ambos os lados da viga e cada um puder resistir a um cisalhamento de 3k N , determine a carga máxima P que pode ser aplica à ext
O elemento consiste em dois canais U de plástico com 12 mm de espessura colados em A e B. Se a carga distribuída tiver intensidade máxima w 0 = 50 k N m , determine a tensão de cisalhamento máxima a q
O elemento consiste em dois canais U de plástico com 12 mm de espessura colados em A e B. Se a cola puder suportar uma tensão de cisalhamento admissível de τ a d m = 4,2M P a , determine a intensidade
O perfil em U é submetido a um cisalhamento V = 75k N . Determine o fluxo de cisalhamento desenvolvido no ponto A