Uma força F = {6i - 2j + 1k} kN produz um momento = {4i + 5j - 14k} kN m em relação à origem das coordenadas, o ponto O. Se a força age em um ponto tendo uma coordenada x de x = 1 m, determine as coordenadas y e z. Nota: a figura mostra F e em uma posição arbitrária.

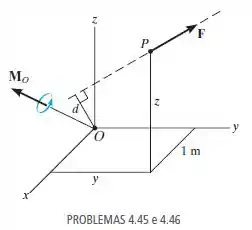
Fonte: Estática Mecânica para Engenharia – 14ª ed

Vamos então aplicar esse determinante:

Assim, temos um sistema de equações:

Temos 2 incógnitas e 3 equações. Então, resolvendo esse sistema, temos:

E