Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 28
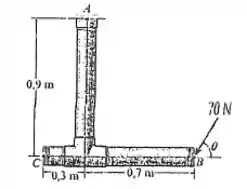
28. A força de age na extremidade do tubo em B. Determine os ângulos da força que produzirá os momentos máximo e mínimo em relação ao ponto A. Quais são as intensidades desses momentos.
Passo 1
Primeiro, o que o enunciado quer saber é qual faz o ser o maior possível e o menor possível.
Concorda comigo que o e menor possível seria igual a , que nada mais é a força não tendo efeito algum na rotação do tubo.
Vamos analisar uma das maneiras calcular , que é dado por:
Sendo a distância perpendicular do eixo (no caso o ponto A) até a linha de ação da força, a força empregada no nosso objeto.
Para o momento máximo ter um valor máximo a linha de ação da força deve ser perpendicular a e para o momento máximo ser zero como foi dito acima, a linha de ação da força deve ser paralela a .
Passo 2
Agora vamos descobrir para que valores de a linha de ação da força é perpendicular e paralela a . Vejamos a seguinte figura:
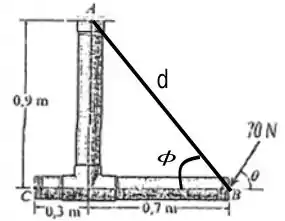
Nela podemos ver o (para saber o valor de basta fazer Pitágoras), e é um ângulo interno triangulo formado.
Você concorda comigo que para a seta que representa a força ser perpendicular a (o ângulo entre eles ser ) a seguinte relação tem que ser satisfeita.
Passo 3
Agora vamos descobrir para que valor de faz com que a seta da força e sejam paralelos.
Você concorda comigo que para a seta que representa a força ser perpendicular a (o ângulo entre eles ser ) a seguinte relação tem que ser satisfeita.
Passo 4
Para acharmos vamos usar uma relação um artifício trigonométrico bem conhecido que é:
Logo:
Passo 5
Assim para o ângulo entre d e a linha da força ser :
Esse valor para faz com que o módulo máximo seja o maior.
E para que a seta da força e d sejam paralelos:
Esse valor para faz com que o módulo máximo seja o menor possível que o caso é .
Passo 6
Agora vamos descobrir a intensidade do momento máximo.
Como o ângulo entre a reta da força e é o momento máximo é dado por:
O valor de é fácil de achar por Pitágoras.
Logo:
A intensidade mínima como já foi falado é:
Resposta
para se obter o valor máximo do momento
para se obter o valor mínimo do momento
Momento máximo
Momento mínimo