Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 63
A força atua sobre o suporte dentro do octante mostrado. Se , e , determine as componentes de .
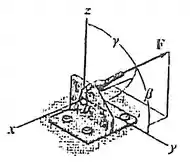
Passo 1
O exercício já nos fornece dois ângulos diretores podemos encontrar o terceiro pela relação:
Logo:
Usamos a raiz negativa pois nossa força aponta no sentido negativo do eixo e nosso ângulo será obtuso.
Passo 2
Agora vamos encontrar as componentes da força através da sua intensidade e dos ângulos que temos:
Resposta
Exercícios de Livros Relacionados
O grampo é usado em uma matriz. Se a força vertical que atua sobre o parafuso é F = { - 500 k } N , determine as intensidades de suas componentes F 1eF 2 que atuam ao longo do eixo O A e perpendicular
Determine as intensidades das componentes da força F = 56N que atuam ao longo e perpendicular à linha A O .
Encontre a intensidade da componente da força projetada ao longo do tubo.
Determine a intensidade, a direção e o sentido da força F → = 240N i → - 270N j → + ( 68 0N ) k → .
Uma barra de aço ABC é sustentada em parte pelo cabo DBE, que passa pelo anel B sem atrito. Sabendo que a tração no cabo é 1712 N, determine os componentes dessa força exercida pelo cabo no suporte em