Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 145

Um único extensômetro de deformação , formando um ângulo de 18° com um plano horizontal, é usado para determinar a pressão do tanque cilíndrico de aço mostrado. O tanque tem espessura uniforme de 6,35   m m , diâmetro de 600   m m e é feito de um açoo E = 200   G P a e ν = 0,30 . Determinar a pressão no tanque, uma vez que o extensômetro nos fornece uma deformação específica de 280 × 10 - 6   m m / m m .

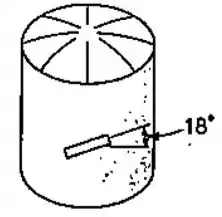
Passo 1

Fala aee!! Vamos resolver mais uma questão de Resmat? Então partiu!

Para fazer essa questão a gente vai precisar fazer o seguinte passo a passo:

  1. Achar as tensões atuantes no vaso de pressão.
  2. Achar as deformações.
  3. Construir o ciclo de Mohr.
  4. Finalmente achar a pressão.

Passo 2

O problema fala de um tanque de paredes finas e para isso a gente sabe, ou deveria saber rs, que:

σ x = σ t a n g e n t e = p r t

σ y = σ c i r c u n f e r e n c i a l = p r 2 t

Além disso a tensão cisalhante é nula

τ x y = 0

Passo 3

Agora vamos achar as deformações a partir das tensões:

ε x = 1 E ⋅ ( σ x - ν ⋅ σ y )

ε x = 1 E ⋅ p r t - ν ⋅ p r 2 t

ε x = p r t ⋅ E ⋅ 1 - ν 2

ε x = 0,85 ⋅ p r t ⋅ E

Para a deformação em y

ε y = 1 E ⋅ ( σ y - ν ⋅ σ x )

ε y = 1 E ⋅ p r 2 t - ν ⋅ p r t

ε y = p r t ⋅ E ⋅ 1 2 - ν

ε y = 0,20 ⋅ p r t ⋅ E

Como não há força de cisalhamento:

γ x y = 0

Passo 4

Agora vamos construir o ciclo de mohr primeiro vamos calcular a deformação média:

ε m é d = ε x + ε y 2

ε m é d = 0,85 ⋅ p r t ⋅ E + 0,20 ⋅ p r t ⋅ E 2

ε m é d = 0,525 ⋅ p r t ⋅ E

Como não há deformação angular γ então o raio é igual a:

R = ε x - ε y 2

R = 0,85 ⋅ p r t ⋅ E - 0,20 ⋅ p r t ⋅ E 2

R = 0,325 ⋅ p r t ⋅ E

Montando o ciclo de Mohr:

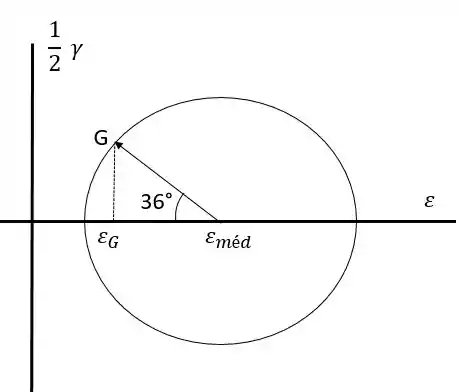
Show, mas de onde surgiu esse ângulo de 50°? Surgiu porque o ângulo dentro do c´rculo de Mohr é o dobro do “real”.

Então quando vai valer a deformação ε G do ponto onde estamos analisando? Para saber isso a gente tem que pegar a projeção horizontal e portanto vai valer:

ε G = ε m é d - R ⋅ c o s ( 36 ° )

ε G = 0,525 ⋅ p r t ⋅ E - 0,325 ⋅ p r t ⋅ E ⋅ 0,8

ε G = 0,262 ⋅ p r t ⋅ E

Passo 5

Para achar a pressão basta reorganizar a equação:

p = 0,262 ⋅ ε G ⋅ t ⋅ E r

substituindo os valores (lembrando que ε G = 280 × 10 - 6   m m / m m , dado problema):

p = 0,262 ⋅ 280 × 10 - 6 ⋅ 0,0635 ⋅ 200 × 10 9 0,3

p = 3,10   M P a

Resposta

p = 3,10   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 ° no sentido anti-horário.
Determine o intervalo de valores de σ x para o qual a tensão de cisalhamento máxima no plano das tensões é igual ou menor que 69M P a .
Para o estado plano de tensão mostrado, determine o maior valor de σ y para o qual a tensão de cisalhamento máxima no plano das tensões é igual ou menor que 75M P a .
As fibras de um elemento de madeira formam um ângulo de 15 ° com a vertical. Para o estado de tensão mostrado, determine (a) a tensão de cisalhamento no plano da tensão paralela às fibras e (b) a tens
Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 ° no sentido anti-horário.