Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 93
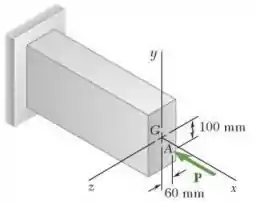
Uma força de compressão excêntrica de é aplicada na extremidade da viga em balanço. Substitua por um sistema força-binário equivalente em .
Passo 1
Como já é conhecido, uma força equivalente pode ser determinada a partir de uma força e de um binário. Por conta disso é possível que o caminho inverso seja feito, ou seja, um sistema força-binário pode ser gerado a partir de uma única força.
Dessa forma, se pretende determinar uma força e um momento gerado por um binário que ajam sobre o mesmo ponto.
Passo 2
Assim, escolhe-se uma força tendo a mesma intensidade e mesmo sentido da força dada no problema, mas com atuação sobre um ponto diferente. No caso, o momento desejado terá atuação sobre o mesmo ponto, este que será a origem de coordenadas .
Passo 3
Logo, os resultados serão dados por:
E, sabendo que o momento é dado por:
Para este caso, o vetor deve partir do ponto até o ponto , já que é o ponto de interesse. Então: