Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 12

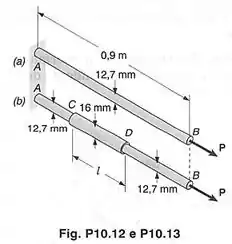
Uma força P de intensidade 10   k N é aplicada em cada uma das barras de aço mostrada. Usando E = 200   G P a , determinar:

  1. a energia de deformação absorvida pela barra a ;
  2. o comprimento necessário l , se a energia de deformação absorvida pela barra b é 90 % da energia de deformação adquirida pela barra a .

Passo 1

E aí, pessoal! Vamos fazer uma questão de energia de deformação pra dominar o assunto?

Primeiro, o enunciado quer que a gente calcule a energia de deformação U a da barra a que está sob carga P = 10   k N . A área A da seção transversal da barra a é constante ao longo de tuda barra. Isso ocorre, pois seu diâmetro D é constante e igual a 12,7   m m . O comprimento L da barra a vale 0,9   m . A figura abaixo mostra a barra a de lado com todos esses dados!

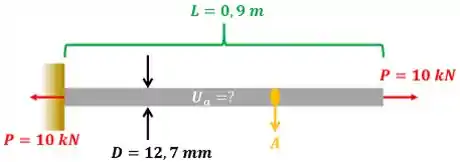
A fórmula que calcula as energias de deformação de barras com áreas da seção transversal constantes é a fórmula 10.14 do livro.

Usaremos essa fórmula para calcular U a .

U a = P 2 L 2 A E

onde E é o módulo de elasticidade do aço que vale 200   G P a segundo o enunciado.

Depois de calcular U a , o exercício pede para a gente calcular o comprimento l que faz a barra b ter 90 % da energia U a da barra a . Ou seja:

U b = 0,9 × U a

Essa barra b pode ser separada em duas barras. Uma barra de comprimento l com diâmetro constante D 1 = 16   m m e área da seção transversal A 1 constante. A outra barra está dividida em duas. No entanto, podemos considerar ela como uma só, porque suas duas partes têm mesmo diâmetro D 2 = 12,7   m m e mesma área A 2 ! O comprimento dessa barra vale L - l .

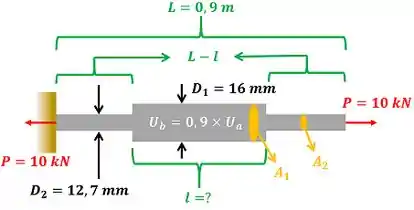
Resumindo, a barra b é formada por duas barras: a barra 2 de comprimento L - l que tem área da seção transversal constante e igual a A 2 e a barra 1 de comprimento l com área de seção transversal A 1 . Como a barra b é formada por duas barras, sua energia de deformação U b é a soma entra as energias de deformação da barra 1 U 1 e da barra 2 U 2 .

U b = U 1 + U 2

Como essas duas barras têm áreas de seção transversal constantes, podemos usar a fórmula 10.14 do livro que calcula as energias de deformação U 1 e U 2 delas.

U 1 = P 2 l 2 A 1 E

U 2 = P 2 L - l 2 A 2 E

Substituindo U 1 e U 2 na equação de U b :

U b = P 2 l 2 A 1 E + P 2 L - l 2 A 2 E

Agora que temos todas essas informações em mãos, vamos calcular a energia de deformação U da barra a no próximo passo!

Passo 2

Nesse passo nós vamos resolver a letra (a) da questão. Ou seja, calcular a energia de deformação U da barra completa. Para isso, a área A em m 2 .

A = π × D 2 4       ⟹       A = π × 12,7 2 4       ⟹       A = 127   m m 2       ⟹       A = 127 × 10 - 6   m 2

Além disso, temos que converter a força P de k N para N , multiplicando P por 10 3 .

P = 1 0   k N       ⟹       P = 1 0 × 10 3   N

Por fim, temos que converter E de G P a para P a , multiplicando E por 10 9 .

E = 200   G P a       ⟹       E = 200 × 10 9   P a

U a = P 2 L 2 A E       ⟹       U a = 1 0 × 10 3 2 × 0,9 2 × 127 × 10 - 6 × 200 × 10 9       ⟹       U a = 1,772   J

Passo 3

Nesse passo nós vamos resolver a letra (b) da questão, calculando l .

Para calcular o comprimento l da barra 1 que faz parte da barra b , precisamos calcular U b pela equação abaixo.

U b = 0,9 × U a       ⟹       U b = 0,9 × 1,772       ⟹       U b = 1,595   J

Agora, precisamos conhecer as área A 1 e A 2 em m 2 para usar a outra fórmula de U b e achar l .

A 1 = π × D 1 2 4       ⟹       A 1 = π × 16 2 4       ⟹       A 1 = 201   m m 2       ⟹       A 1 = 201 × 10 - 6   m 2

A 2 = π × D 2 2 4       ⟹       A 2 = π × 12,7 2 4       ⟹       A 2 = 127   m m 2       ⟹       A 2 = 127 × 10 - 6   m 2

Substituindo esses valores na outra fórmula de U b , achamos:

U b = P 2 l 2 A 1 E + P 2 L - l 2 A 2 E

1,595   = 10 × 10 3 2 × l 2 × 201 × 10 - 6 × 200 × 10 9 + 10 × 10 3 2 × 0,9 - l 2 × 127 × 10 - 6 × 200 × 10 9

1,595 = 1,2438 × l + 1 , 9685 × 0,9 - l

Isolando o l , encontramos:

l ≈ 0,25   m

Aeeee! O sufoco valeu a pena! Terminamos!

Resposta

a   U a = 1,772   J

b   l ≈ 0,25   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra cilíndrica AB tem um comprimento L de 1,83m e um diâmetro de 32m m . Ela é feita de um aço doce, que é assumido ser elastoplástico com E = 200G P a e σ e = 250M P a . Uma força P é a aplicad
Uma força axial centrada P é aplicada à barra de aço mostrada. Sabendo-se que σ a d m = 165M P a e b = 75m m , determinar:O maior valor admissível para PO menor valor permissível de r f para que no ar
Uma força axial centrada P, de itensidade P = 90k N , é aplicada à barra de mostrada. Sabendo-se que b = 90m m , determine A máxima tensão normal no furoO menor valor permissível de r f se a máxima te
Uma força axial centrada P é aplicada à barra de aço mostrada. Sabendo-se que σ a d m = 165M P a e b = 75m m , determinar:O maior valor admissível para PO menor valor permissível de r f para que no ar
Uma barra cilíndrica A B tem um comprimento L de 1,50m e um diâmetro de 20m m . Ela é feita de um aço doce, que é assumido ser elastoplástico com E = 200G P a e σ e = 250M P a . Uma força P é aplicada