Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 6
O diagrama tensão-deformação mostrado foi desenhado a partir dos dados obtidos durante um ensaio de tração de um corpo de prova de uma liga de alumínio. Usando , determinar:
- o módulo de resiliência da liga;
- por meio aproximado o módulo de tenacidade da liga.
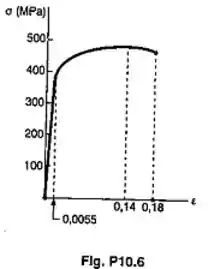
Passo 1
E aí, pessoas! Estudando muito?
O exercício quer que a gente calcule o valor módulo de resliliência e do módulo de tenacidade de uma liga de alumínio. O módulo de resiliência de qualquer material é igual à área embaixo da reta de um diagrama tensão-deformação . Esse diagrama e os dados que a questão nos informa para calcular são mostrados abaixo.
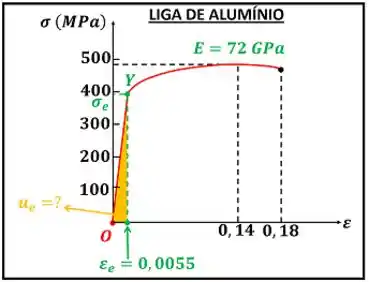
é a tensão de escoamento do material. é o módulo de elasticidade do material. é a deformação a partir da qual o material começa a escoar.
O módulo de resiliência é uma área muito pequena pintada de laranja.
O módulo de tenacidade é toda a área sob a curva do diagrama tensão-deformação.
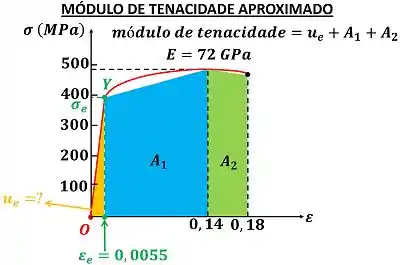
Para calcular aproximadamente o módulo de tenacidade da liga, temos que somar o módulo de resiliência com as áreas de dois trapézios e .
Resumindo, tanto para calcular o módulo de resiliência quanto para calcular o módulo de tenacidade, precisamos calcular as áreas sob as curvas. Vamos começar calculando o .
Passo 2
Para calcular , precisamos saber quanto vale a tensão de escoamento da liga, porque é a altura do triângulo que forma a área sob a reta ! A base desse triângulo é igual a .
A figura abaixo mostra a área exagerada do triângulo que fica abaixo de .
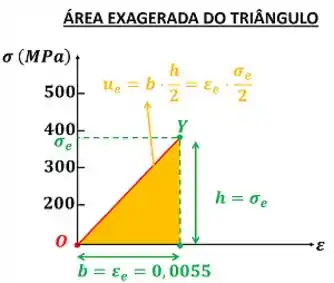
Vimos agora que para achar , precisamos achar . A fórmula da tensão de escoamento em função de se encontra abaixo.
No entanto, para usar essa fórmula temos que converter de para , multiplicando o valor em por .
Pronto, enfim podemos achar .
Substituindo esse valor na fórmula de presente no gráfico, achamos:
Podemos converter esse resultado de para , dividindo por .
Passo 3
Agora, vamos calcular o módulo d etenacidade nesse passo. Para isso, temos que achar as áreas e dos trapézios. A fórmula da área dos trapézios é base maior mais base menor , vezes altura do trapézio dividido por .
No caso dos trapézios, a altura não são valores de tensão , mas sim diferenças entre valores de deformação . As tensões são as bases e . Esses valores de tensão que representam as bases e do trapézio são aproximados encontrados através da visualização do gráfico.
Isso fica mais claro olhando para a figura abaixo.
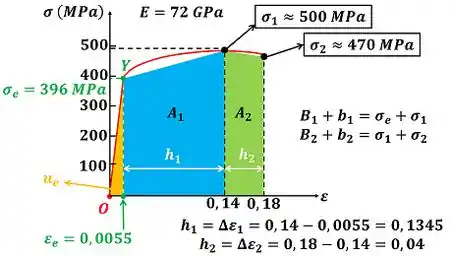
Antes de utilizar as informações da figura, temos que converter as tensões , de para , multiplicando as tensões por .
Agora sim, usando as informações presentes na figura, achamos:
Cuidado! O valor de que devemos colocar na fórmula do módulo de tenacidade deve estar em !
Como o módulo de tenacidade é a soma de todas as áreas, encontramos: