Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 98b
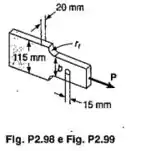
Uma força axial centrada P é aplicada à barra de aço mostrada. Sabendo-se que e , determinar:
- O maior valor admissível para P
- O menor valor permissível de para que no arredondamento a tensão normal admissível não seja excedida com a aplicação da carga P encontrada no item a)
Passo 1
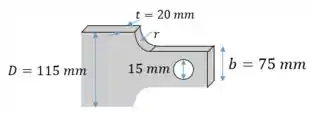
Da mesma forma que o item anterior, vamos começar calculando a concentração de tensão!
Mas como ainda não temos o valor do raio, vamos calcular o coeficiente através da equação da tensão:
Isolando o :
Aplicando os valores:
Passo 2
Agora vamos dar uma olhada no Gráfico de Concentração de Tensões:
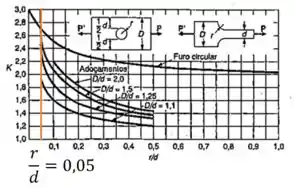
Perceba que a curva fica assintótica. Dessa forma, qualquer valor de estará relacionado a razão:
Então podemos calcular o raio:
Resposta
Exercícios de Livros Relacionados
O estado de tensões mostrado ocorre em um componente de máquina, que é feito de um aço para o qual σ e = 41 5M P a . Usando o critério da máxima energia de distorção, determinar a variação dos valores
O bloco E desloca-se com uma velocidade v 0 = 3,6m / s quando choca-se perpendicularmente à placa B D que está presa na extremidade das barras A B e C D . Sabendo-se que as barras são feitas de um aço
Um colar D de 6k g tem uma velocidade v 0 = 4,5m / s , quando ele se com uma pequena placa presa na extremidade A da barra A B , de diâmetro 20m m . Usando-se E = 200G P a , determinar:a carga estátic
Para a viga prismática mostrada, determinar a declividade no ponto D .
Para a viga prismática mostrada, determinar a deflexão na extremidade A .