Uma barra cilíndrica AB tem um comprimento de e um diâmetro de . Ela é feita de um aço doce, que é assumido ser elastoplástico com e . Uma força P é a aplicada na barra até sua extremidade descer de um valor . Determinar o máximo valor da força e deformação permanente da barra, depois que a força for removida, sabendo-se que
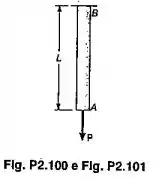
Passo 1
Vamos começar a questão calculando a área de seção transversal da barra:
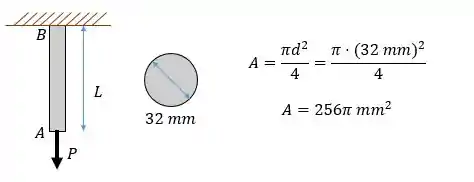
Passo 2
Ao atingir o valor da tensão de escoamento a força se torna constante. Em outras palavras, quando se atinge o comportamento plástico, o valor da força não depende da deformação.
Então podemos calcular:
Isolamos o
Aplicando os valores:
Passo 3
Agora vamos determinar qual é a maior deformação elástica possível:
E podemos calcular o maior alongamento elástico:
Passo 4
A questão nos dá o valor da deformação máxima. Vamos usar isso para a deformação permanente da barra:
Item A)
Passo 5
Item B)
Resposta