Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 47
Uma força F com intensidade F = 100 N age ao longo da diagonal do paralelepípedo. Determine o
momento de F em relação ao ponto A, usando e .
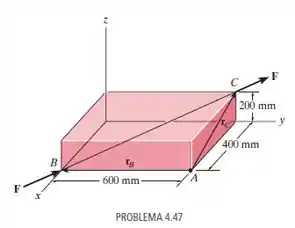
Fonte: Estática Mecânica para Engenharia – 14ª ed
Passo 1
Fala aí, tudo bem até agora?!
Esperamos que sim haha!!
Bem, o problema nos dá a Força aplicada e nos pede o Momento em A em relação a B e a C, separadamente. Vamos utilizar aquele passo a passo que estamos nos acostumando a fazer.
Podemos então, aplicar a eq. 4.7 do livro texto, a equação do momento de uma força em relação a um ponto, e ver como fica:
Passo 2
Mas primeiro vamos encontrar o vetor posição :
Observemos que a Força F é de B em relação a C. E para encontrar a Força em coordenadas cartesianas, precisamos de:
Assim, podemos encontrar a Força F em coordenadas cartesianas:
Passo 3
Então, primeiro fazendo o momento em relação a C, utilizaremos o vetor :
Assim, aplicando o determinante, temos:
E, fazendo o momento em relação a B, utilizaremos o vetor :
Assim, aplicando o determinante, temos:
Resposta
Portanto: