Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 32

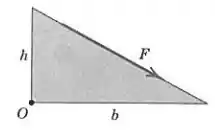
A força de módulo F atua ao longo da aresta da placa triangular. Determine o momento de F em relação ao ponto O .

Passo 1

O vetor unitário   n na direção e sentido da força F é escrito assim:

n = b   i - h   j b 2 + h 2

Então, o vetor de F pode ser dado dessa forma:

F = F n

F = F b   i - h   j b 2 + h 2

Passo 2

Agora, escolhemos um ponto ao longo da linha de ação da força F , por exemplo, ( 0 , h ) , para calcular o momento por meio da fórmula:

M O = r × F

M O = h   j × F b   i - h   j b 2 + h 2

M O = F h b 2 + h 2 j × b   i - h   j

M O = F h b 2 + h 2 - b   k

M O = - F b h b 2 + h 2   k

Ou seja, temos um momento no sentido horário com módulo:

M O = F b h b 2 + h 2

Resposta

M O = F b h b 2 + h 2 no sentido horário

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento da força de 50N (a) em relação ao ponto O , usando o teorema de Varignon e(b) em relação ao ponto C , por um enfoque vetorial.
A força F de 10k N é aplicada no ponto A . Calcule o momento de F em relação ao ponto O . Determine os pontos nos eixos x e y em relação aos quais o momento de F vale zero.
À medida que um trailer é puxado para frente, a força F = 500N é aplicada à esfera do reboque do trailer, como mostrado. Determine o momento dessa força em relação ao ponto O .
Um mecânico puxa a chave de boca de 13m m com a força de 140N mostrada. Determine o momento dessa força em relação ao centro O do parafuso.
Parte de um separador mecânico de moedas funciona como se segue: Moedas de um e dez centavos rolam por um plano inclinado de 20 ° , sendo que a parte triangular final do separador gira livremente em r