Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 38
À medida que um trailer é puxado para frente, a força é aplicada à esfera do reboque do trailer, como mostrado. Determine o momento dessa força em relação ao ponto .
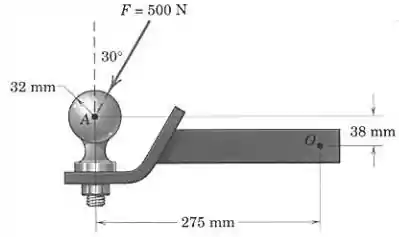
Passo 1
Nesse caso, podemos decompor a força de em uma força horizontal para a esquerda e uma força vertical para baixo, conforme mostra a figura a seguir:
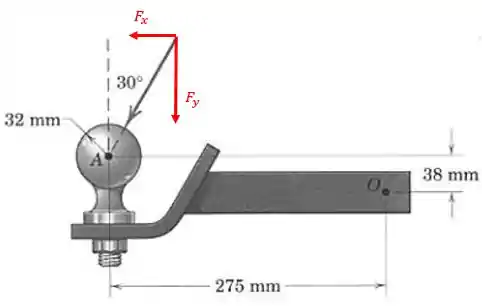
Sendo o ponto de aplicação da força, temos que está agindo a uma distância vertical de do ponto e a uma distância horizontal de , ambas para o sentido anti-horário. Logo,
Resposta
(sentido anti-horário)
Exercícios de Livros Relacionados
Para arrancar o prego em B , a força F exercida sobre o cabo do martelo precisa produzir um momento no sentido horário de 60N ∙ m em relação ao ponto A . Determine a intensidade necessária da força F
Dados os três vetores não nulos A , B e C , mostre que se A ∙ B × C = 0 , os três vetores necessitam estar no mesmo plano.
Se o momento produzido pela força de 4k N em relação ao ponto A é 10k N . m no sentido horário, determine o ângulo θ , onde 0 ° ≤ θ ≤ 90 ° .
Se A , B e D são vetores, prove a propriedade distributiva para o produto vetorial, ou seja, A × B + D = A × B + ( A × D ) .
Prove a identidade do produto triplo escalar A ∙ B × C = A × B ∙ C .