Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 72
Se a força resultante que atua sobre o gancho é N, determine a intensidade e os ângulos de direção coordenados de .
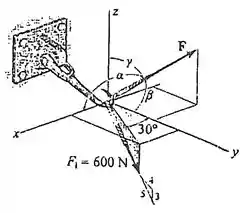
Passo 1
Queremos encontrar a força dadas as forças e .
Antes, vamos decompor nas suas componentes, de início já podemos encontrar a direção , dada a relação por cateto e hipotenusa dada pelo triângulo da força com o plano :
Já, a projeção no plano é dada por:
E então decompomos em e :
Temos em
E temos em :
E o vetor cartesiano de fica:
Perceba que a direção é negativa de acordo com o sentido negativo da força no eixo .
Passo 2
Vamos agora encontrar as componentes da força , dado:
E a intensidade do seu módulo será:
Passo 3
Só falta encontrar os ângulos de direção coordenados de , sendo:
Então:
Resposta
Exercícios de Livros Relacionados
Determine a intensidade e os ângulos diretores coordenados da força resultante, e desenhe esse vetor no sistema de coordenadas.
O parafuso está submetido à força F, que tem componentes atuando ao longo dos eixos x, y, z, como mostra a figura. Se a intensidade de F é 80N, α= 60 ° e γ= 45 ° , determine as intensidades de suas co
O tarugo montado no torno está sujeito a uma força de 60 N. Determine o ângulo diretor coordenado b e expresse a força como um vetor cartesiano.
Determine os comprimentos dos fios AD, BD e CD. O anel em D está a meio caminho entre A e B.