Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 71

Se α = 120 ° ,   β < 90 ° ,   γ = 60   ° e F = 400   N , determine a intensidade e os ângulos de direção coordenados da força resultante que atua sobre o gancho.

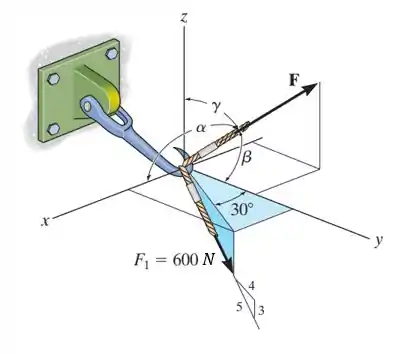
Passo 1

A força resultante F R será a soma das forças F com F 1 de forma que:

F R → = F → + F 1 →

Para somar as duas forças da forma como elas estão no desenho nós teremos que fazer a soma vetorial delas.

Projetando a força F de 400   N nos três eixos coordenados nós teremos:

F = 400   cos ⁡ α i ^ + cos ⁡ β j ^ + cos ⁡ γ k ^

Onde α ,   β e γ são ângulos diretores do vetor unitário de F , ou seja:

cos 2 ⁡ α + cos 2 ⁡ β + cos 2 ⁡ γ = 1

Então:

cos ⁡ β = 1 - cos 2 ⁡ α - cos 2 ⁡ γ = 1 - cos 2 ⁡ 120 - cos 2 ⁡ 60

β = cos - 1 ⁡ 1 - cos 2 ⁡ 120 - cos 2 ⁡ 60 = 45 °

Uma vez que β < 90 ° , não podendo ser 135 ° ,

F = 400   cos ⁡ 120 i ^ + cos ⁡ 45 j ^ + cos ⁡ 60 k ^

Passo 2

Agora vetorizando F 1 , nós temos:

F 1 = 600   4 5 s e n   30   i ^ + 4 5 cos ⁡ 30 j ^ - 3 5 k ^  

Primeiro temos que projetar no plano x y ao fazer a projeção no triângulo 3,4,5 (cujo cosseno diretor é 4 / 5 ) e depois projetar com o ângulo de 30 ° para os eixos x e y ) e depois projetar para z com o ângulo do triângulo 3,4 , 5 cujo cosseno diretor é 3 / 5 para z negativo. Isso no deixa com:

F 1 = 120 4 s e n   30   i ^ + 4 cos ⁡ 30 j ^ - 3 k ^

Somando então F 1 com F de modo a querer encontrar a força resultante nós temos:

F R = F 1 + F

F R = 120 4 s e n   30   i ^ + 4 cos ⁡ 30 j ^ - 3 k ^ + 400   cos ⁡ 120 i ^ + cos ⁡ 45 j ^ + cos ⁡ 60 k ^

F R = 120 ⋅ 4   s e n   30 + 400 cos ⁡ 120 i ^ + 120 ⋅ 4 cos ⁡ 30 + 400 cos ⁡ 45 j ^ + 400 cos ⁡ 60 - 3 ⋅ 120 k ^

Fazendo essa conta temos:

F R = 40 i ^ + 698.53 j ^ - 160 k ^   [ N ]

Os componentes dessa força resultante podem ser entendidas como:

F R = F x i ^ + F y j ^ + F z k ^

Passo 3

A intensidade dessa força será dada por:

F = 40 2 + 698.53 2 + 160 2 = 717.74   N

Então os ângulos diretores (que são parecidos com os ângulos de F 1 saca? São os ângulos cujo cosseno projeta o vetor diretor da força para os eixos coordenados) serão iguais a:

α = cos - 1 ⁡   F x F R = cos - 1 ⁡ 40 717.74 = 86.81   °

β = cos - 1 ⁡ F y F R = cos - 1 ⁡ 698.53 717.74 = 13.29 °

γ = cos - 1 ⁡ F z F R = cos - 1 ⁡ - 160 717.74 = 102.88 °

Resposta

Intensidade da força: 717.74   N

Ângulos diretores:

α = 86.81   °

β = 13.29 °

γ = 102.88 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a intensidade e os ângulos diretores coordenados da força resultante no ponto A do poste.
A corda exerce uma força F = {12i + 9j - 8k} kN sobre o gancho. Se a corda tem 4 m de extensão, determine o local x,y do ponto de conexão B e a altura z do chão até o gancho..
cabo com 8 m de extensão está fixado ao solo em A. Se z = 5 m, determine o local +x, +y do ponto A. Escolha um valor de modo que x = y.
Determine o ângulo  θ( 0 ° ≤ θ ≤ 90 ° ) para a estrutura AB, de modo que a força horizontal de 400 N  tenha uma componente de  500 N direcionada de A para C. Qual  é  a componente da  força que  atua