Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 56
As três forças concorrentes que atuam sobre o poste produzem uma força resultante . Se e estiver a de , como mostra a figura, determine a intensidade necessária de expressa em função de e do ângulo .
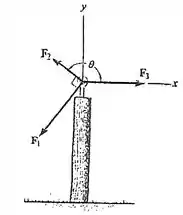
Passo 1
Aqui nossa , que bom né, pelo menos o poste não cai, temos então:
Vamos começar pelas componentes em :
Perceba que faz um ângulo com a vertical, enquanto faz 90° com , por ângulos suplementares podemos usar o mesmo ângulo que faz com a vertical, apenas alterando para seno a fim de encontrar a componente do , fica então:
Sabendo que :
Fazendo o arcotangente de :
Passo 2
Agora vamos para as componentes em :
Lembrando que faz 90° com para usar o mesmo ângulo e inverter as relações trigonométricas na componente de :
Resposta
Exercícios de Livros Relacionados
Sob condições não uniformes e escorregadias da estrada, as duas forças mostradas são exercidas sobre as duas rodas de tração traseiras da caminhonete, que tem um diferencial traseiro que limita derrap
Ao empurrar uma mesa na direção da porta de saída, três estudantes exercem as forças mostradas na vista de topo. Determine o sistema força-binário equivalente no ponto A . Determine, então, a equação
Determine e localize a resultante R das duas forças e do momento atuando na viga em I .
Determine a resultante R das três forças atuando no olhal. Ache também o módulo de R e o ângulo θ x que a resultante faz com o eixo x .
Determine o sistema força-binário equivalente na origem O para cada um dos três casos de forças sendo aplicadas nas arestas de uma placa quadrada de lado b .