Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 110

A força  F  tem um módulo de 2   k N e é direcionado de   A   para  B . Calcule a projeção  F C D   d e   F  sobre a linha  C D  e determine o ângulo  θ   entre  F  e  C D .

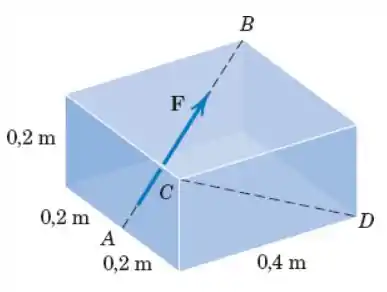
Passo 1

Primeiramente, como vamos precisar do vetor A B e depois da sua projeção em C D vamos escrever as coordenadas de todos esses pontos adotando o vértice logo antes de A como origem do sistema de coordenadas, então, teremos

A = 0,0.2,0.2 B = - 0.4,0 , 0.2 C = 0,0.4,0.2 D = - 0.4,0.4,0

Assim, nosso vetor unitário na direção a b vai ser dado por

n a b → = - 0,4 i - 0,2 j + 0,2 k 0,4 2 + 0,2 2 + 0,2 2 = 0,82 i - 0,41 j + 0,41 k

Como, nosso vetor F tem módulo 2 k N podemos escrever F como sendo

F → = 2 k N ⋅ 0,82 i - 0,41 j + 0,41 k = - 1,64 i - 0,82 j + 0,82 k

Passo 2

Para fazer a projeção vamos precisar do vetor unitário na direção C D que vai ser dado por

n a b → = - 0,4 i - 0,2 j 0,4 2 + 0,2 2 = - 0,8 9 i - 0,4 4 j

Dessa forma, nossa projeção vai ser dada por

F C D = - 1,64 i - 0,82 j + 0,82 k ⋅ - 0,89 i - 0,44 j

F C D = 1,4596 - 0,3608 = 1,0988 ≈ 6 5   k N

Passo 3

Bom, observando agora a figura podemos escrever o vetor C D → que será dado por

C D → = - 0,4 i - 0,2 k     m m

Com isso, conseguimos determinar o ângulo entre a força de 2 k N e a linha C D por meio da seguinte fórmula

θ = a r c o s   F → ⋅ C D → F C D →

θ = a r c o s   - 1,64 ⋅ - 0 , 89 - 0,82 ⋅ 0 + 0,82 ⋅ - 0,44 2 000

θ ≈ 8 9 , 97 °

Pronto, tá resolvido nosso exercício. 😜

Resposta

F C D = 6 5   k N ,   θ ≈ 89,97 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro de tração traseira está atolado na neve entre outros carros estacionados como mostrado. Em uma tentativa de livrar o carro, três estudantes exercem forças no carro nos pontos A ,BeC , enquant
Expresse uma força F de 900 N vetorialmente em termos dos vetores unitários i ,jek . Determine a projeção entre F e o eixo y .
A força trativa no cabo de sustentação em A vale 2k N . Expresse a tensão T em forma vetorial.
Determine a resultante R das duas forças aplicadas no suporte. Descreva R em termos de vetores unitários ao longo dos eixos, x e y mostrados.
Expresse em notação de vetor a força R exercida na polia pelas duas tensões, se as forças T são iguais a 400N no cabo da polia. Determine o módulo de R .