Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 109
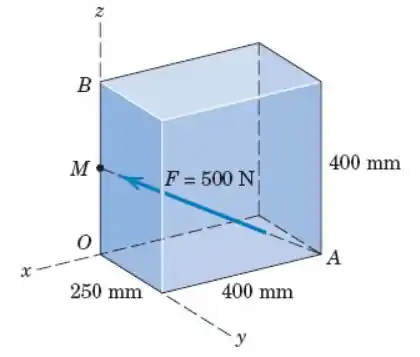
A força tem um módulo de e atua ao longo da diagonal da linha , em que é o ponto médio do lado vertical do paralelepípedo. Expresse em termos de seu módulo multiplicado pelo vetor unitário apropriado, e determine seus componentes escalares.
Passo 1
E aí meus queridxs, como vocês estão?
Vamos lá, nossa questão é bem rapidinha, então, vamos direto ao ponto. Primeiramente vamos escrever as coordenadas dos pontos e que serão dados por
Agora, colocando de forma vetorial teremos
E agora para encontrar o vetor unitário é só dividir pelo próprio módulo
Dessa forma, teremos
Passo 2
E como a força tem módulo (fornecida e aponta na direção de
Sendo assim, nossos componentes escalares serão
Pronto, tá resolvido nosso problema.
Resposta
Exercícios de Livros Relacionados
Determine os componentes da força F de 800N ao longo dos eixos oblíquos a e b . Também determine as projeções de F sobre os eixos a e b .
Determine as componentes x e y da força trativa T que é aplicada no ponto A da barra O A . Despreze os efeitos da pequena polia em B . Assuma que r e θ são conhecidos.
Os cabos de sustentação A B e A C estão presos no topo da torre de transmissão. A força trativa no cabo A B vale 8k N . Determine a força trativa T necessária no cabo A C , tal que o efeito resultante
A placa retangular é composta de quadrados de 1f t , como mostrado. Uma força de 30l b é aplicada no ponto A na direção mostrada. Calcule o momento M O da força em relação ao ponto B por pelo menos do
A tensão no cabo A B é 100N . Determine o momento em relação à O desta tensão aplicada ao ponto A da barra em forma de T . A dimensão b é 600m m .