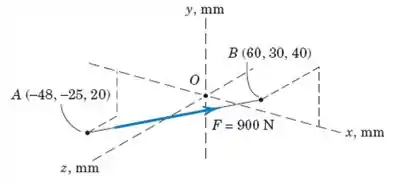
Expresse uma força  de vetorialmente em termos dos vetores unitários . Determine a projeção entre  e o eixo 

E aí meus queridos, tudo bem com vocês? Preparados pra mais uma questãozinha?

Prestem bastante atenção que essa questão é relativamente rapidinha, porém, precisa de um pouco da nossa atenção para que a gente não se perca no meio do caminho. Primeiro de tudo vamos escrever o vetor unitário da direção de que será dado por

Pois bem, para escrevermos de forma vetorial basta multiplicarmos nosso vetor unitário pelo módulo da nossa força. Sendo assim, teremos

Além disso, para concluirmos nosso exercício, precisamos encontrar a projeção no eixo que nada mais é do que a nossa componente da notação vetorial de . Sendo assim, nossa projeção será

Voilà! Tá resolvido nosso problema.