Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 57

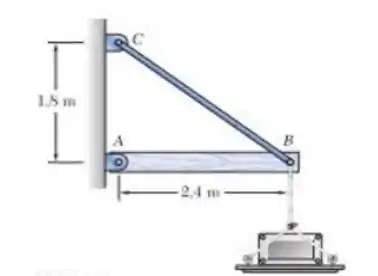
Uma plataforma de 40 kg está presa à extremidade B de uma barra AB de madeira, de 50 kg, suportada, conforme mostra a figura, por um pino em A e por uma barra esbelta de aço BC com um limite de carga de 12 kN. (a) Utilizando o método do coeficiente de Projeto para Carga e Resistência, com um coeficiente de resistência ∅ = 0,90 e coeficiente de carga y p = 1,25 e y E = 1,6, determine a maior carga que pode ser colocada com segurança na plataforma. (b) Qual é o coeficiente de segurança convencional correspondente para a barra BC?

Passo 1

E aii gurizada, tudo belezinha? Espero que sim!!! Vamos desenhar antes de mais nada nosso famoso diagrama de corpo livre :D

Então vamos realizar o somatório do momento em A:

∑ M A   = F × d =   0

∑ M A   =   ( 2 , 4 ) 3 5   P   –   2 , 4   W 1   -   1 , 2   W 2

∴ P =   5 3   W 1 +   5 6   W 2

Passo 2

Então agora podemos encontrar W 1 e W 2 , partiu!

W 1 =   ( 40 ) × ( 9,81 )   =   392,4 N

, W 2   =   ( 50 ) × ( 9,81 )   =   490,5 N

Para encontrarmos o valor de P temos que fazer a seguinte consideração:

P D =   5 3 ( 392,4 )   +   5 6 ( 490,5 )   =   1,0628   X   10 3 N

Onde:

W 1 =   m g  

W 2 =   0

P L =   5 3 m g

m   =   3 5 ×   P L g

γ D P D   +   γ L P L   =   ∅ P U

P L =   ∅ P U - γ D P D γ L =   0,90 12   X   10 3 - 1,25 ( 1,0628   X   10 - 3 ) 1,6

=   5,920   X     10 3 N

Passo 3

  1. Para encontrarmos o carregamento, antes devemos determinar a massa:

    2.   m   = 3 5 × 5,92   X   10 3 9,81 = 362   k g

    P   =   P D   +   P L   =   1,0628   X   10 3   +   5,920   X   10 3 = 6,983   X   10 3 N

    Passo 3

    Para o cálculo do fator de segurança:

  2. F . S .   =   P U P   = 12   X   10 3 6,983   X   10 3

F . S .   =   1,718

Resposta

  1. m= 362 kg
  2. F.S. = 1,718
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas placas de cobertura, cada uma com 16m m de espessura, são soldadas a uma viga de perfil laminado W690 × 125 , como mostrado. Sabendo-se que l = 4,4 m e b = 300m m , determinar a máxima tensão nor
Sabendo-se que σ a d m = 160M P a e τ a d m = 100M P a , selecionar o perfil I de abas largas que poderia ser usado para suportar o carregamento mostrado.
Para a viga com o carregamento mostrado, dimensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 860k P a .
Para a viga com o carregamento mostrado, dimensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 860k P a .
Sabendo-se que σ a d m = 16 5M P a e τ a d m = 100M P a , selecionar o perfil I de abas largas que poderia ser usado para suportar o carregamento mostrado.