Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 56

Em um projeto alternativo para a estrutura do Problema 1.55, deve ser utilizado um pino de 10 mm de diâmetro em A. Supondo que todas as outras especificações permaneçam inalteradas, determine a carga P admissível se adotarmos um coeficiente global de segurança de 3,0.

Passo 1

Eai gurizada beleza?? Primeiramente use ABC como corpo livre.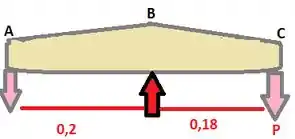

Fazendo o somatório do momento em B e A temos:

∑ M B   = F × d =   0 :     0,20 F A   –   0,18 P   =   0       P   =   10 9   F A

∑ M A   =   F × d = 0 :     0,20 F B D   –   0,38 P   =   0     P   =   10 19   F B D

Considerando o cisalhamento duplo no pino A, a área é calculada como:

A   =   π 4   d 2   =   π 4   ( 0,010 ) 2   =   78,54   x   10 - 6 m 2

Agora podemos determinar FA e P, vejam :D

F A   =   2 τ ∪ A F . S .   =   2 100 X 10 6 ( 78,54   X   10 - 6 ) 3,0   =   5,236   X   10 3 N

P   = 10 9 × F A = 5,82   X   10 3 N

Passo 2

Com base no cisalhamento duplo nos pinos B e D,a área é calculada como:

  A   =   π 4 d 2   =   π 4 ( 0,012 ) 2   =   113,10   X   10 - 6 m 2

Agora podemos determinar FBD e P, vejam :D

F B D   =   2 τ ∪ A F . S .   =   2 100 X 10 6 ( 113,10   X   10 - 6 ) 3.0   =   7,54   X   10 3 N

P   =   10 9   F B D   =   3,97   X   10 3 N

Passo 3

Com base na compactação nos vínculos BD, para um vínculo

  A   =   ( 0,020 ) × ( 0,008 )   =   160   X   10 - 6 m 2

F B D   =   2 σ U A F . S .   =   2 250   X   10 6 160   X   10 - 6 3,0   =   26,7   X   10 3 N

P   =   10 9   F B D   =   14 , 04   X   10 3 N

Resposta

P = 3,97 kN

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo-se que σ a d m = 160M P a e τ a d m = 100M P a , selecionar o perfil I de abas largas que poderia ser usado para suportar o carregamento mostrado.
Determine as equações das curvas dos diagramas da força cortante e do momento fletor, para a viga com carregamento indicado. (Adotar a origem no ponto A.)
Usando o método da Sec 7.4, resolver o prob. 7.25
Usando o método da Sec 7.4, resolver o prob. 7.23
Usando o método da Sec. 7.4, resolver o Prob. 7.14