Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 23
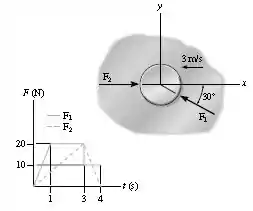
As forças e variam como mostra o gráfico. O disco liso de desloca-se para a esquerda com uma velocidade escalar de , quando . Determine a intensidade e a direção da velocidade vetorial do disco quando .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Pensa comigo... O impulso gerado por e no período de tempo é igual a área sob o gráfico para cada um. Vamos calcular.
A área sob o gráfico de é dada por:
A área sob o gráfico de é dada por:
Passo 2
Vamos analisar o diagrama de corpo livre do sistema:
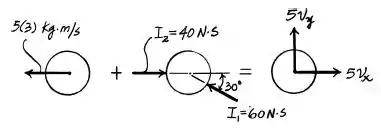
Analisando em temos:
Analisando em temos:
Passo 3
A magnitude de é:
A direção com a horizontal é dada por:
Resposta
Exercícios de Livros Relacionados
As três esferas idênticas de aço estão soldadas às duas barras de massa desprezível formando uma unidade rígida. O conjunto é liberado a partir do repouso na posição mostrada e desliza no plano vertic
As três barras idênticas, cada uma com massa de 8k g , são unidas pelos dois conectores livremente articulados de massa desprezível e estão em repouso sobre uma superfície horizontal lisa. Calcule a a
Calcule a aceleração do centro de massa do sistema de quatro cilindro de 10k g . Despreze o atrito e a massa das polias e cabos.
As duas esferas de 2k g estão inicialmente em repouso sobre a superfície horizontal quando uma força vertical F = 60N é aplicada à junção dos fios aos quais estão conectadas como mostrado. Calcule a c
Para o sistema de partículas do Prob. 4/1, determine H G e H ˙ G .