Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 101
Um garfo é usado para mover a partícula lisa de 1 kg em torno da trajetória no formato de um limaçon (caracol de Pascal), m. Se rad, onde é dado em segundos, determine a força que o garfo exerce sobre a partícula no instante s. O garfo e a trajetória contatam a partícula somente em um lado.
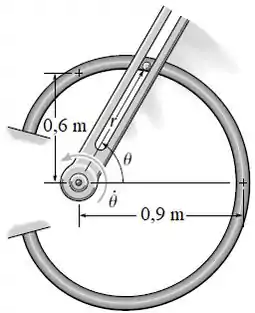
Passo 1
O Problema nos deu as seguintes informações:
Massa de partícula:
Ângulo:
A questão pede para determinarmos a força exercida pelo garfo sobre a partícula no instante s.
Em , temos que rad.
Desenhamos o seguinte diagrama de corpo livre:
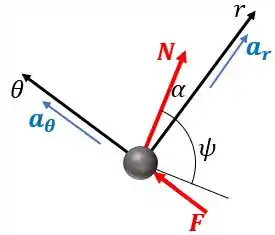
Onde é a força normal e é a força exercida pela barra.
Passo 2
Sabemos que a trajetória é definida por
Portanto, as derivadas temporais em são:
As derivadas temporais em são:
Em , temos que
Para
Passo 3
Sabemos que as componentes da aceleração nas coordenadas e são dadas por
Logo,
Passo 4
Agora vamos descobrir o ângulo com que a força normal é aplicada à partícula.
Visto que a trajetória já está especificada, o ângulo que a linha radial deformada forma com a tangente pode ser determinado pela equação
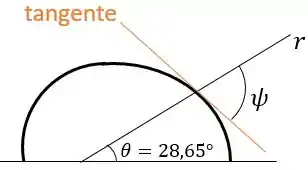
Temos que , logo
Portanto, para , temos que
atua perpendicular à tangente à curva em . Logo, o ângulo entre a força e o eixo é igual à
Passo 5
Aplicaremos as Equações do Movimento.
Analisando no eixo , temos que
Analisando no eixo , temos que
O sinal negativo de indica que esta força está agindo na mesma direção, porém no sentido contrário ao desenhado no diagrama de corpo livre.