Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 91
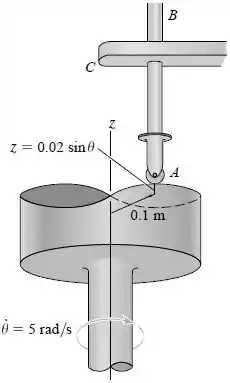
A barra de 2 kg desloca-se para cima e para baixo à medida que sua extremidade desliza sobre a superfície lisa do came, onde m e m. Se o came está girando com velocidade angular constante de 5 rad/s, determine a força máxima e mínima que o came exerce sobre o rolete . Despreze o atrito no apoio e a massa do rolete.
Passo 1
O enunciado nos dá as seguintes informações:
Massa da barra :
Velocidade angular do came:
O fato da velocidade do came ser constante nos diz que a derivada de no tempo é igual a zero, ou seja, .
Além disso, sabemos que
Analisando o desenho do enunciado, vemos que a barra se move somente na direção do eixo . Portanto, seu diagrama de corpo livre será da seguinte forma:
Onde é a força peso, e é a força normal exercida no rolete devido a superfície do came.
O enunciado pede para determinarmos a força máxima e mínima exercida sobre o rolete.
Passo 2
Primeiramente, vamos encontrar as derivadas temporais em ( e ). Como , temos que
Agora analisaremos as derivadas temporais em ( e ). O valor de é conhecido e constante, logo
Em seguida, vamos encontrar as derivadas temporais em ( e ). Sabemos que , logo
Passo 3
Sabemos que a componente da aceleração no eixo é dada por
Logo,
Como ,
Passo 4
Agora aplicaremos as Equações do Movimento.
Analisando no eixo , temos
Conhecemos o valores de e de , portanto, para encontrar os valores máximos e mínimos da força , devemos saber quais são os valores máximo e mínimo de .
Sabemos que depende de e que seus valores de máximo e mínimo ocorrem quando . Logo,
Para :
Para :
Portanto, teremos os seguintes valores para :