Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 20

O volante A de 15 kg tem um raio de giração em relação a seu centro de 100 mm. O disco B tem uma massa de 25 kg e está acoplado ao volante através de uma correia que não desliza em suas superfícies de contato. Se um motor fornece ao volante um torque no sentido anti-horário M = 75 t N . m , onde t é dado em segundos, detemrine o tempo necessário para o disco alcançar uma velocidade angular de 60 rad/s partindo do repouso.

Passo 1

Começaremos o exercício calculando o momento de massa do volante ao redor do ponto C:

I C = m k C 2 = 15 0,1 2

I C = 0,15   k g . m 2

Podemos também já calcular o momento de inércia do disco ao redor do ponto D:

I D = 1 2 m r 2 = 1 2 25 0,225 2

I D = 0,6328   k g . m 2

Passo 2

Sabemos também que podemos relacionar as velocidades do volante A e do disco B da seguinte forma:

ω A r A = ω B r B

Sendo assim, podemos encontrar a velocidade angular final do volante A:

ω A 0,15 = 60 ( 0,225 )

ω A = 90   r a d / s

Passo 3

Agora podemos aplicar o princípio do impulso e da quantidade de movimento angular para o volante A com o auxílio do esquema a seguir:

↺ +   I C ω 1 + ∑ ∫ t 1 t 2 M C d t = I C ω 2

0 + ∫ 0 t 75 t d t + ∫ T 2 d t 0,15 - ∫ T 1 d t 0,15 = 0,15 ( 90 )

37,5 t 2 + 0,15 ∫ T 2 - T 1 d t = 13,5

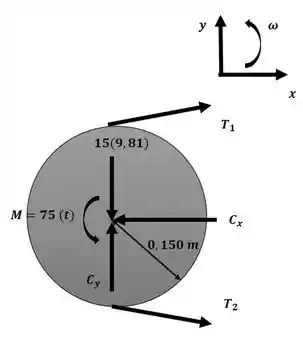
Essa será nossa equação número 1. Agora podemos aplicar o mesmo princípio para o disco B com o auxílio da imagem a seguir:

↺ +   I D ω 1 + ∑ ∫ t 1 t 2 M D d t = I D ω 2

0 + ∫ T 1 d t 0,225 - ∫ T 2 d t 0,225 = 0,6328 ( 60 )

∫ T 2 - T 1 d t = - 37,968

Substituindo essa equação na equação número 1, é possível encontrar o tempo necessário pedido no enunciado:

37,5 t 2 + 0,15 ∫ T 2 - T 1 d t = 13,5

37,5 t 2 + 0,15 ( - 37,968 ) = 13,5

t = 0,715   s

Resposta

t = 0,715   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O aro circular leve de raio r carrega uma tira uniforme pesada de massa m em torno da metade de sua circunferência e é liberado a partir do repouso sobre a inclinação na posição superior mostrada. Apó
Um telescópio espacial é apresentado na figura, um dos volantes de reação de seu sistema de controle de orientação angular está girando a 10r a d / s conforme indicado, e nessa velocidade o atrito no
O regulador mecânico de esferas opera com um eixo vertical O - O . Quando a velocidade no eixo N é aumentada, o raio de rotação das duas esferas de 1,5 kg tende a aumentar, e a massa A de 0 kg é eleva
Em uma atração acrobática, um homem de massa m A pula de uma plataforma elevada sobre a extremidade da viga leve, porem resistente, com uma velocidade v 0 . O menino de massa m B é lançado para cima c
O carro com tração nas rodas traseiras possui uma massa de 1600 kg com centro de massa em G . O coeficiente de atrito efetivo entre os pneus e a estrada é de 0.80 . considere o carro e as rodas como u