Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 105

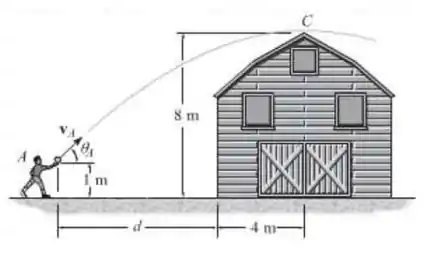
Um garoto em A tenta jogar uma bola sobre o telhado de um celeiro com uma velocidade escalar inicial de v A = 15   m / s . Determine o ângulo θ A no qual a bola deve ser jogada de maneira que ela alcance sua altura máxima em C. Encontre também a distância d de onde o garoto deve ficar para fazer o lançamento.

Passo 1

Temos um problema de lançamento oblíquo. Uma bola percorrerá uma distância no plano x y . Calma. Podemos dividir este problema em dois outros problemas: um no eixo x e outro no eixo y . No eixo x a velocidade é constante e no eixo y a partícula está sujeita a ação da gravidade. Portanto, vamos analisar cada caso separadamente!

Passo 2

Vamos analisar inicialmente o seu deslocamento no eixo y . Mas calma lá, muito cuidado nesta hora!!! A posição final da bola será s = 8   m . E a posição inicial? s 0 = 0   m ??? Não! A resposta é simples e clara, não! Olhem o desenho com calma e percebam que s 0 = 1   m . Isto é, a bola não parte do solo. Agora sim, utilizando as equações da cinemática, temos:

s = s 0 + v y t + a t 2 2

8 = 1 + v A ⋅ sen ⁡ θ A ⋅ t - g t 2 2

7 = 15 ⋅ sen ⁡ θ A t - 4,905 ⋅ t 2

Bom, chegamos em uma equação que relaciona o ângulo θ A com o tempo t , precisamos então determinar outra equação para poder resolver esse nosso problema.

Passo 3

Temos um problema agora. Qual será a outra equação para relacionarmos o ângulo θ A com o tempo t ? Se pensarmos em relação ao eixo x , uma outra variável aparecerá (a variável d, que por sinal iremos calcular jajá!). E agora? O que fazer?

A chave para esta pergunta está no enunciado da questão. A bola atinge altura máxima em C. Se ele atinge altura máxima, significa que temos um ponto crítico! Isto é:

d s d t = 0

E quem é a derivada da função posição no tempo??? Isto mesmo! A velocidade!!! Portanto, no ponto C, temos v = 0 ! Agora simmm! Vamos conseguir mais uma equação. A partir da cinemática, temos:

v = v 0 + a t

0 = v A ⋅ sen ⁡ θ A - g t

t = 1,53 sen ⁡ θ A

Substituindo esta relação na equação do Passo 1, teremos:

7 = 15 ⋅ sen ⁡ θ A ⋅ 1,53 sen ⁡ θ A - 4,905 ⋅ ( 1,53 sen ⁡ θ A ) 2

11,47 sen 2 ⁡ θ A = 7

Portanto,

sen ⁡ θ A = 0,781

θ A = 51,4 °

Além disto, temos que t = 1,195   s

Passo 4

Para calcularmos a distância d, basta utilizarmos o valor de t = 1,195   s na equação da posição da bola no eixo x . Portanto, temos:

s = s 0 + v x t

d + 4 = 0 + 15 ⋅ cos ⁡ 51,4 ° ⋅ 1,195

d = 7,18   m

Resposta

θ A = 51,4 °

d = 7,18   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A cavilha P é inpulsionada pelo anel do garfo O A ao longo da trajetória curva descrita por r = e θ . Quando θ = π / 4 rad, o anel tem uma velocidade angular e a aceleração angular de θ ˙ = 2 rad/s e
A plataforma está girando em torno do eixo vertical de modo que em qualquer instante a sua posição angular é θ = ( 4 t 3 / 2 ) , onde t é dado em segundos. Uma bola rola para fora ao longo do sulco ra
Na parte baixa do loop em um plano vertical, um aeroplano tem velocidade de 150 m/s e está acelerando a uma taxa de 25 m/s2. O raio de curvatura do loop é 2.000 m. O aeroplano está sendo controlado pe
A partir de medições de uma fotografia, verificou-se que o fluxo de água mostrado na figura deixa o bocal em A e tem raio de curvatura de 25 m. Determine (a) a velocidade inicial vA do fluxo, (b) o ra
Um morador usa o removedor de neve para limpar a entrada de sua garagem. Sabendo que a neve é lançada a um ângulo médio de 40° com a horizontal, determine a velocidade inicial v0 da neve.