Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 34

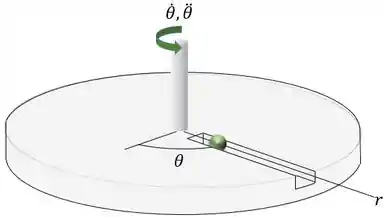
A plataforma está girando em torno do eixo vertical de modo que em qualquer instante a sua posição angular é θ = ( 4 t 3 / 2 ) , onde t é dado em segundos. Uma bola rola para fora ao longo do sulco radial de maneira que sua posição é dada por r = 0,1 t 3 , onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da bola quando t = 1,5 s.

Passo 1

O enunciado nos dá as seguintes informações:

Posição angular da plataforma: θ = 4 t 3 / 2 rad;

Posição da bola: r = 0,1 t 3 m;

Para t = 1,5 s, devemos determinar a intensidade da velocidade e da aceleração da bola.

Vamos utilizar coordenadas polares para resolver essa questão.

Passo 2

Primeiramente, vamos encontrar a intensidade da velocidade da bola.

Sabemos que, por definição, a velocidade em coordenadas polares é composta por uma componente radial e uma componente transversal, conforme exibido abaixo:

v = v r 2 + v θ 2

Onde

v r = r ˙

v θ = r θ ˙

Logo, para encontrar o valor de v , precisamos definir quem são r ˙ e θ ˙ .

Sabendo que r = 0,1 t 3 , sua derivada temporal será

r ˙ = d r d t = 0,3 t 2

Sabendo que θ = 4 t 3 / 2 , sua derivada temporal será

θ ˙ = d θ d t = 6 t 1 / 2 = 6 t

Logo, as componentes radial e transversal da velocidade são:

v r = r ˙ = 0,3 t 2

v θ = 0,1 t 3 6 t = 0,6 t 7 / 2

A intensidade de v   é dada por

v = 0,3 t 2 2 + 0,6 t 7 2 2

v = 0,09 t 4 + 0,36 t 7

Em t = 1,5 s, obteremos

v = 0,09 ( 1,5 ) 4 + 0,36 ( 1,5 ) 7

v = 2,57   m / s

Passo 3

Agora vamos encontrar a intensidade da aceleração da bola.

Sabemos que, por definição, a aceleração em coordenadas polares é composta por uma componente radial e uma componente transversal, conforme exibido abaixo:

a = a r 2 + a θ 2

Onde

a r = r ¨ - r θ ˙ 2

a θ = r θ ¨ + 2 r ˙ θ ˙

Logo, para encontrar o valor de a , precisamos definir quem são r ˙ , r ¨ , θ ˙ e θ ¨ .

Sabendo que r = 0,1 t 3 , suas derivadas temporais são

r ˙ = d r d t = 0,3 t 2

r ¨ = d 2 r d t 2 = 0,6 t

Sabendo que θ = 4 t 3 / 2 , suas derivadas temporais são

θ ˙ = d θ d t = 6 t 1 / 2 = 6 t

θ ¨ = d 2 θ d t 2 = 3 t - 1 / 2 = 3 t

Logo, as componentes radial e transversal da aceleração são:

a r = r ¨ - r θ ˙ 2 = 0,6 t - 0,1 t 3 6 t 2 = 0,6 t - 3,6 t 4

a θ = r θ ¨ + 2 r ˙ θ ˙ = 0,1 t 3 3 t + 2 0,3 t 2 6 t = 0,3 t 5 2 + 3,6 t 5 2

A intensidade de a   é dada por

a = 0,6 t - 3 , 6 t 4 2 + 0,3 t 5 2 + 3,6 t 7 2 2

Em t = 1,5 s, obteremos

a = [ 0,6 ( 1,5 ) - 3 , 6 ( 1,5 ) 4 ] 2 + [ 0,3 ( 1,5 ) 5 2 + 3,6 ( 1,5 ) 7 2 ] 2

a = [ - 17,325 ] 2 + [ 10,7471 ] 2

a = 20,39   m / s 2

Resposta

v = 2,57   m / s

a = 20,4   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um projétil é disparado com uma velocidade u na entrada A de um túnel horizontal de comprimento L e altura H . Determine o valor mínimo de u e o valor correspondente do ângulo θ para o qual o projétil
Um projétil é disparado com uma velocidade u perpendicular ao declive, que está inclinado de um ângulo θ com a horizontal. Derive uma expressão para a distância R até o ponto de impacto.
Determine a localização h do ponto em direção ao qual o arremessador deve lançar a bola de modo que ela atinja a mão do receptor. A bola é lançada com uma velocidade de 40m / s .
Para atender a critérios de projeto, pequenas esferas de rolamento devem saltar através de uma abertura de tamanho limitado no topo de sua trajetória após repercutir a partir de uma chapa inerte como
Um jogador de ferradura lança a ferradura em A com uma velocidade inicial v 0 = 11m / s . Determine a faixa para o ângulo de lançamento θ para o qual a ferradura baterá na estaca vertical de 350m m .