Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 192
A gôndola de inspeção para um cabo suspenso está sendo puxada para cima no cabo inclinado à velocidade de . Se o cabo de controle em de repente se rompe, calcule o tempo após a ruptura ocorrer para a gôndola atingir uma velocidade de para baixo no cabo inclinado. Despreze o atrito e trate a gôndola como uma partícula.
Passo 1
É importante perceber que, quando o cabo de controle se rompe, a gôndola não cai na vertical, mas desliza livremente pela corda!
Nós sabemos que (como podemos desprezar o atrito) a única força realizando trabalho sobre a gôndola é a componente do peso na direção da corda, então vamos começar calculando isso.
Está vendo aquele triângulo retângulo na figura? É ele quem vai nos dar a dica de como calcular essa componente.
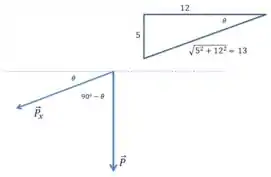
Passo 2
Beleza, então agora nosso problema é: quanto tempo essa força leva para aumentar a velocidade da gôndola de para (estamos considerando o sentido negativo como sendo para cima na direção do cabo).
Usando o teorema do impulso, temos a seguinte expressão:
Resposta
A velocidade é alcançando após segundos.