Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 196
O corpo em forma de projétil com massa tem uma anilha com massa colocada sobre seu diâmetro escalonado. Conforme o conjunto passa descendo por uma abetura com velocidade , a anilha atinge a superfície firme e é deixada para trás. Se o tempo de duração do impacto é , determine a força total exercida sobre a anilha pela superfície e a perda percentual de energia cinética do sistema.
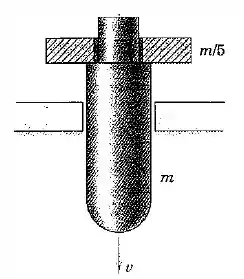
Passo 1
Vamos supôr que a força exercida sobre a anilha no intervalo é constante. Nesse caso, durante o contato as forças que agiam sobre a anilha eram:
Onde definimos o sentido positivo como sendo vertical para baixo. Pelo teorema do impulso podemos fazer a seguinte afirmação:
Ou seja, a força tem o seguinte valor:
Passo 2
Agora vamos analisar a perda de energia nesse processo. Inicialmente, quando o corpo e a anilha estavam se movendo juntos com velocidade , a energia total do sistema era:
Depois, quando apenas o corpo se move com a velocidade (já que a anilha foi parada pela força ):
Então a perda relativa de energia é:
O que equivale a uma perda percentual:
Resposta
e .