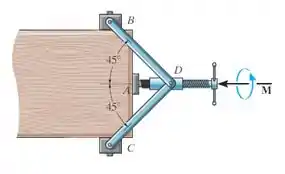
O grampo fornece pressão de várias direções nas bordas da prancha. Se o parafuso de rosca quadrada tem um passo de , raio médio de e o coeficiente de atrito estático é , determine a força horizontal desenvolvida na prancha em e as forças verticais desenvolvidas em se um torque é aplicado à manivela para apertá-la ainda mais. Os blocos em são conectados à prancha por pinos.
Passo 1
Um bom início de questão para mecânica é sempre que possível (na maior parte das vezes vai ser) desenhar o diagrama de corpo livre do objeto em questão. Isso vai nos ajudar e muito a entender o que se passa na questão e o que queremos encontrar!
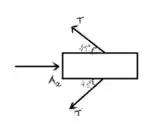
Passo 2
Galera, para um parafuso de rosca quadrada, o ângulo de passo é determinado a partir de . Aqui, é o passo da rosca e é o raio médio da rosca. Tendo essa ideia em mente, vamos calcular o ângulo de passo da nossa questão:
Passo 3
O ângulo de atrito estático para o parafuso de rosca quadrada é dado por . Logo,
Passo 4
Vamos dizer que . Assim, a equação para o momento do parafuso é dada por:
Substituindo os valores na equação, temos:
Passo 5
Agora só nos resta descobrir os valores das forças verticais em e . Para isso precisamos descobrir o valor de (expresso no diagrama de corpo livre), uma vez que
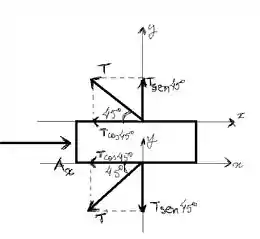
Para um sistema em equilíbrio, sabemos que o somatório da forças que atuam sobre um objeto é igual a erro. Assim, assumindo como referencial positivo o sentido para direita, o somatório das forças no eixo é:
Assim, as forças verticais em são iguais a:
Resposta
A força desenvolvida em é igual a:
As forças verticais em e são iguais a: