Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 140
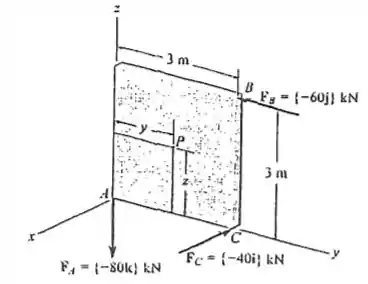
Substitua as três forças atuando na chapa por um torsor. Especifique a intensidade da força e o momento de binário para o torsor e o ponto onde sua linha de ação intercepta a chapa.
Passo 1
Desejamos substituir as três forças por um torsor, assim, precisamos especificar a intensidade da força e o momento binário para o torsor e as coordenadas do ponto onde sua ação intercepta a chapa. Nossa é dada por
Tomando o vetor unitário da direção da força resultante vamos ter
Podemos fazer a decomposição do momento ao longo das direções e adotar que ele está atuando na direção de
Resolvendo o sistema composto pelas equações descritas acima vamos obter
Resposta
Exercícios de Livros Relacionados
Três forças paralelas do parafuso atuam sobre a chapa circular. Determine a força resultante e especifique sua posição ( x ,z ) sobre a chapa. F A = 1000N , F B = 500N e F C = 2000N .
A laje da construção está sujeita a quatro cargas paralelas das colunas. Determine a força resultante equivalente e especifique sua posição x ,y sobre a laje. Considere F 1 = 30k N e F 2 = 40k N .
Três forças paralelas do parafuso atuam sobre a chapa circular. Se a força em A possui uma intensidade F A = 1000N , determine as intensidades de F B e F C de modo que a força resultante F R do sistem
Determine as coordenadas do ponto no plano x z pelo qual passa a linha de ação da resultante do sistema de forças, para o sistema de forças do Prob. 2/149.
A resultante das duas forças e do torque pode ser representada por um torçor. Determine a expressão vetorial para o momento M do torçor e encontre as coordenadas do ponto P no plano x z pelo qual pass