Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 88

O grampo mostrado na figura é frequentemente usado em operações de soldagem. Determine a força de aperto sobre as duas peças metálicas em E e os módulos das forças suportadas pelos pinos A , B e D .

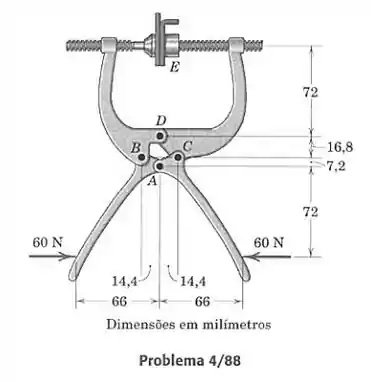
Passo 1

Usando a simetria do grampo, vamos isolar os 2 corpos que compõem a parte da direita, tentando representar as forças que atuam em cada um deles. A parte de cima sofre forças em E e nos pinos B e D . A parte de baixo sofre a força de 60 N e também reações dos pinos em A e B . Devemos prestar atenção na lei da ação e reação para representar o sentido das forças de contato entre as partes, e notar que todas as forças são horizontais, pois se não fossem não teria como haver equilíbrio para os pinos.

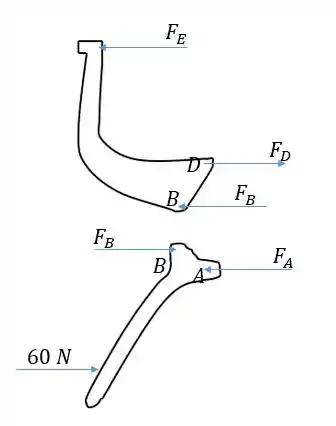
Passo 2

Vamos primeiro fazer as equações para o corpo de baixo, que só tem 2 incógnitas. Fazendo o momento em torno de A , encontramos F B diretamente:

∑ M A = 0 ⇒ - 7,2 F B + 72 × 60 = 0 ⇒ 7,2 F B = 72 × 60

⇒ F B = 72 × 60 7,2 ⇒ F B = 600   N

Agora fazendo a soma das forças horizontais encontramos F A :

∑ F x = 0 ⇒ 60 + F B - F A = 0 ⇒ F A = 60 + 600 ⇒ F A = 660   N

Passo 3

Agora fazemos para o corpo de cima. Encontramos F E fazendo o momento em torno de D :

∑ M D = 0 ⇒ 72 F E - 16,8 F B = 0 ⇒ 72 F E = 16,8 F B

Substituindo pelo valor que encontramos de F B :

72 F E = 16,8 × 600 ⇒ F E = 10080 72 = 140   N

Fazendo agora a soma das forças horizontais ser zero:

∑ F x = 0 ⇒ - F E - F B + F D = 0 ⇒ F D = F E + F B

⇒ F D = 140 + 600 = 740   N

Resposta

F B = 600   N

F A = 660   N

F E = 140   N

F D = 740   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

44. Uma força F → = 6 i - 2 j + 1 kk N produz um momento M 0 = 4 i + 5 j - 14 kk N ⋅ m em relação a origem das coordenadas, o ponto O. Se a força age em um ponto tendo uma coordenada x de x = 1m , det
39. Determine o momento resultante produzido pelas duas forças em relação ao ponto O. Expresse o resultado como um vetor cartesiano.
49. A força F age perpendicularmente ao plano inclinado. Determine o momento produzido por F em relação ao ponto B. Expresse o resultado como um vetor cartesiano.
40. Determine o momento produzido por F B → em relação ao ponto O. Expresse o resultado como um vetor cartesiano.
48. A força F age perpendicularmente ao plano inclinado. Determine o momento produzido por F em relação ao ponto A. Expresse o resultado como um vetor cartesiano.