Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 93
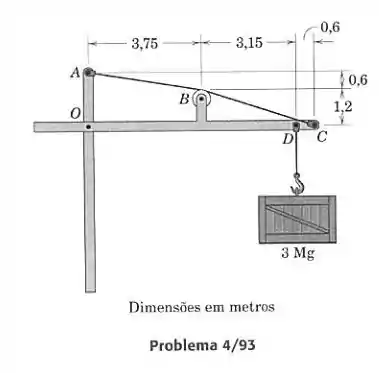
O guindaste simples suporta uma carga de 3 Mg. Determine a força de tração no cabo e o módulo da reação do pino em .
Passo 1
Primeiro devemos decidir quais corpos vamos isolar para satisfazer as equações de equilíbrio. Para evitar várias forças de tração com diferentes ângulos, podemos considerar como um único corpo a barra , a polia em e a parte do fio que estã entre e . Assim, só atuam no corpo a reação em , a carga em e a tração em apontando para :
Passo 2
Agora obteremos diretamente fazendo ser zero o momento em torno de . Precisamos do ângulo que faz com a horizontal:
Então podemos resolver. Temos que lembrar que
Se g = 9,81 m/s²:
Passo 3
Achamos e fazendo o equilíbrio das forças verticais e horizontais:
O valor negativo indica que a força é na verdade para baixo. Agora calculamos o módulo: