Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 45

A viga é composta por três tiras de poliestireno coladas como mostra a figura. Se a cola tiver uma resistência ao cisalhamento de , determine a carga máxima P que pode ser aplicada sem que a cola perca sua capacidade de aderência.

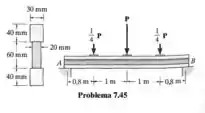
Passo 1

Dados da questão:

A questão pede o máximo valor de

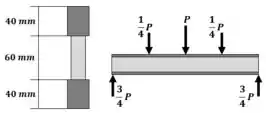
Vamos começar calculando os esforços internos da viga, depois calcularemos as propriedades geométricas da seção transversal: Momento de Inércia e Momento Estático, como a seção é simétrica, já sabemos que o centroide esta no meio da seção.

Por fim, utilizamos a equação de cisalhamento para calcular a carga

Passo 2

Fazemos um diagrama de corpo livre e calculamos as reações de apoio.

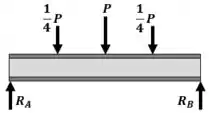
Como o carregamento e as reações são simétricos, podemos garantir que:

Utilizando as reações de apoio, podemos construir o diagrama de esforço cortante. Com ele observamos que o maior esforço cortante é

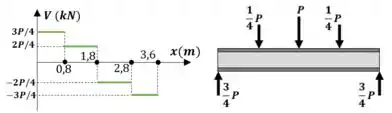
Passo 3

Vamos calcular agora o momento de inércia da seção transversal

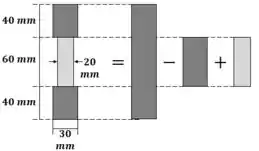
Passo 4

Para calcular o momento estático, vamos considerar a seção em destaque:

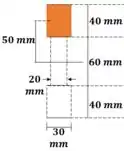
Passo 5

Observe a figura abaixo. O fluxo de cisalhamento na região selecionada “atravessa” uma região com cola.

Pela fórmula do cisalhamento temos:

Substituindo o valor do esforço cortante

Isolando o :

Observe novamente a imagem, perceba que o fluxo de cisalhamento passa por duas regiões de espessuras diferentes. Em situações como essa, devemos selecionar a espessura mais fina, pois ela é mais frágil. Assim, o valor de .