Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 22
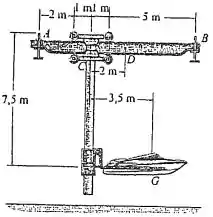
Um guindaste suporta um barco de com o centro de massa em . Determine a força normal interna, o esforço cortante e o momento no ponto da viga mestra. O carrinho está livre para rolar pelo trilho da viga mestra e está localizado na posição indicada. Somente reações verticais ocorrem em e .
Passo 1
Fala, querido!
Ele pede os esforços internos em Para resolver esse tipo de questão tem um passo a passo. Só seguir que dá bom:
- Fazer DCL
- Achar reações nos apoios necessárias
- seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas de cada membro seccionado.
E o que é legal é que essa análise é feita com as queridinhas equações de equilíbrio.
Vamos entender essa estrutura. Ela tem reações verticais apenas em e .
Lembra que para determinar o esforço em uma seção, a gente pode cortar nosso elemento e olhar só para um lado. A única exigência é que conheçamos todas as forças e cargas aplicadas nesse lado que ficou.
Agora olha para nossa figura, se a gente a cortar em e olhar só para a direita, podemos determinar os esforços em . Tudo que precisamos achar é a reação em .
Então essa é a nossa reação necessária para achar. Vamos começar por ela.
Bora!
Passo 2
Para iniciar, podemos analisar o DCL do sistema todo:
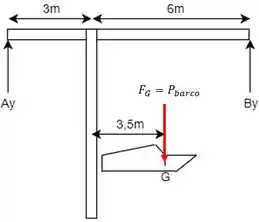
Tal que, aplicando o somatório de momentos em relação ao ponto e considerando o sentido anti-horário como positivo:
Passo 3
Agora, como se deseja encontrar as reações internas em deve-se seccionar o guindaste neste ponto e analisar a seção . Colocamos então as componentes dos esforços internos na seção e os achamos pelas equações de equilíbrio.
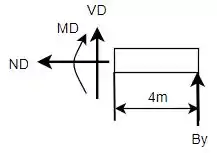
E, então, se torna possível montar as equações de equilíbrio novamente.
Para o eixo , se tem:
Para o eixo :
E, novamente, considerando o sentido anti-horário como positivo:
O sinal negativo mostra que o esforço cortante age no sentido oposto ao convencionado, ou seja, para cima.