Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 20
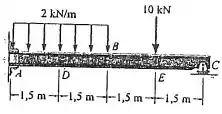
Determine a força normal interna, o esforço cortante e o momento nos pontos e na viga composta. O ponto está localizado à esquerda da carga concentrada de . Assuma que o apoio em seja fixo e a vinculação em seja um pino.
Passo 1
Falaa! O problema quer que a gente encontre os esforços internos em e . Para isso, a gente só precisa achar as reações em um dos lados da viga antes, e depois analisar cada seção.
Repara que temos uma viga com engaste (reação vertical e de momento) numa extremidade e um apoio de primeiro gênero no outro (uma reação vertical). E temos um pino em .
Como a viga é composta, a gente vai dividir em duas partes para analisar as reações, e . A parte não fica em pé sozinha, então a gente vai começar por ela.
Uma coisa importante: ele diz que o ponto está localizado a esquerda da carga concentrada de . Guarda isso no seu coração.
Vem ver como fica!
Passo 2
Para iniciar, podemos analisar a seção que será dada por:
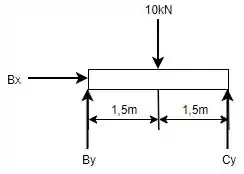
Repara que em temos as reações nas duas direções representando o pino em .
Tal que, aplicando as equações de equilíbrio, tem-se para o eixo :
E, considerando o sentido anti-horário como positivo:
Além de:
Repara, que com isso, a gente acha as reações da direita para a parte da viga, que são as reações no apoio . E também acha as reações da direita para a parte da viga, que são as reações no pino .
Com isso, a gente parte para a analise das seções!
Passo 3
Vamos começar pela seção A gente vai cortar nossa viga nessa seção e olhar só para a direita, onde as forças são conhecidas. Aí a gente posiciona o cortante e o momento nessa seção, seguindo a convenção de sentidos positivos, e os acha pelas equações de equilíbrio.
A partir dos valores das resultantes encontradas e fazendo o DCL da seção , obtém-se:
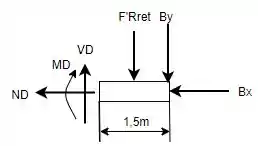
Aqui podemos perceber que as forças internas no ponto mudaram de sentido em relação ao DCL da viga já que estamos olhando uma parte de agora.
Repara que a gente posiciona o cortante e o momento no sentido positivo. Quando a gente corta a viga e olha para a direita, a convenção do cortante positivo na seção é para cima e o momento é no sentido horário, assim:
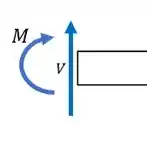
Para o eixo :
Essa força resultante é a força resultante do carregamento distribuído sobre . Continuando:
E, novamente, considerando o sentido anti-horário como positivo:
O sinal negativo mostra que o momento age no sentido oposto ao convencionado.
Passo 4
Analogamente, pode-se fazer o mesmo processo na seção , já que temos o valor da força em . Vamos cortar a viga em e olhar para direita. Será obtido:
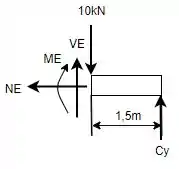
Lembra que o enunciado diz que a seção fica a esquerda da força concentrada de ? Então, se a gente corta nossa viga em e olha para a direita, essa bonita de vai aparecer no nosso DCL, porque ela está a direita de .
Aplicando as equações de equilíbrio obtém-se para o eixo :
E, aplicando o princípio dos momentos em relação ao ponto e considerando o sentido anti-horário como sendo positivo: