Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 54

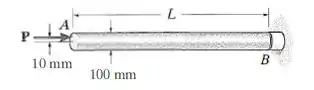
A haste de bronze está engastada em uma extremidade e livre na outra. Se seu comprimento for L = 2 m, determine a maior carga admissível P que pode ser aplicada de modo que ela não sofra flambagem ou escoamento. Calcule também a maior deflexão lateral da haste devido à carga. E = 101 G P a , σ y = 69 M P a .

Passo 1

Calculando primeiro o peso crítico, teremos:

P c r = π 2 E I y k L 2 = 305823,63 k N

A tensão crítica será:

σ c r = P c r A = 38,94 M P a < σ y = 69 M P a

Portanto, podemos calcular alguns parâmetros:

r x = I x A = 25 m m

c = d 2 = 50 m m

e y = 10 m m

Sabemos que:

σ y = P A ( 1 + e y c r x 2 sec ⁡ k L 2 r x P E A

Logo, substituindo e simplificando, teremos:

69 = P A 1 + 0,8 sec ⁡ 0,25173 P E A

Esta equação não é tão simples de resolver, mas como não é nosso foco aqui, utilizaremos um programa para resolvê-la. Isolando-se P A :

P A = 22,1162 M P a < σ y = 69 M P a

Podemos então calcular o valor de P:

P = 22,1162 π × 50 2 = 173,7 k N

Como devemos escolher o menor valor de P:

P = 173,7 k N

Passo 2

A deflexão máxima é dada por:

v m á x = e sec ⁡ P E A k L 2 - 1

Substituindo, teremos:

v m á x = 16,5 m m

Resposta

P = 173,7 k N

v m á x = 16,5 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A coluna W200 × 71 de aço estrutural A-36 está engastada na base e presa por pinos no topo. Se for submetida a carga excêntrica de 375 kN, determine se ela falha por escoamento. A coluna não sofre fla
A coluna de madeira está engastada na base e podemos considerar que está acoplada por pinos no topo. Determine a carga excêntrica máxima P que pode ser aplicada sem provocar flambagem ou escoamento.E
A haste de bronze está engastada em uma extremidade e livre na outra. Se for aplicada a carga excêntrica P= 200k N , determine o maior comprimento admissível L da haste de modo que não sofra flambagem
Uma coluna W360 × 45 de aço estrututral A-36 está engastada na base e livre no topo e tem comprimento L = 6,9 m. Determine a carga excêntrica máxima P que pode ser aplicada de modo que a coluna não so
A haste de alumínio está engastada na base e livre no topo. Se for aplicada a carga excêntrica P = 200 kN, determine o maior comprimento admissível L da haste de modo que ela não sofra flambagem ou es