Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 68
A haste de alumínio está engastada na base e livre no topo. Se for aplicada a carga excêntrica P = 200 kN, determine o maior comprimento admissível L da haste de modo que ela não sofra flambagem ou escoamento.
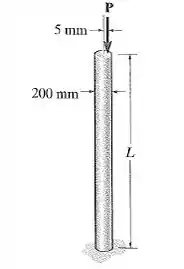
Passo 1
Falaaa! Vamos reunir nossos dados:
Vamos precisar do momento de inércia da seção também.
E como ela está engastada numa extremidade e livre na outra, .
Temos uma carga excêntrica em relação ao eixo . Mas ela é simples em relação a . Em cada situação usamos uma fórmula diferente, por isso, precisamos separar esse exercício em dois casos.
Mas em ambos os casos, o que a gente quer é encontrar que não permita nem a flambagem nem o escoamento da coluna, belezinha?
Passo 2
Primeiramente, vamos tratar da flambagem no eixo. A fórmula do peso crítico sem excentricidade para esse eixo é:
Como queremos o maior para essa situação, nossa carga crítica vai ser o do enunciado. Substituindo os dados e isolando , teremos:
A tensão causada por essa carga é:
Como ela é menor que , essa carga não causa escoamento. E nosso comprimento achado é válido.
Passo 3
No eixo , temos a excentricidade . Por isso devemos calcular alguns parâmetros para usar na fórmulinha:
Esse é a maior distância do eixo até a borda da seção.
A fórmulinha que a gente tem para esse caso com , é a fórmula da tensão
Como a gente quer o que não causa escoamento, vamos usar a tensão de escoamento nessa fórmulinha para achar
Substituindo nossos dados e isolando-se o , teremos:
Resolvendo isso, chegaremos em:
Devemos escolher o menor valor de que achamos, então ficamos com: