Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 35
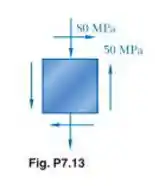
Resolva o Problema 7.13 usando o círculo de Mohr.
Passo 1
Beleza! Através do estado de tensões que foi dado no enunciado, conseguimos esboçar o círculo de Mohr para esse estado. A partir do círculo, podemos encontrar a inclinação dos planos principais e suas tensões. Depois disso vamos rotacionar o elemento diferencial e desenhar os novos pontos no círculo de Mohr para então encontrar as tensões normal e de cisalhamento para as duas rotações pedidas.
Passo 2
Tá legal! Vamos começar calculando a tensão média, que é dada por:
Substituindo os valores conhecidos, teremos:
Agora, vamos escrever as coordenadas dos pontos para o círculo de Mohr, no nosso caso, temos:
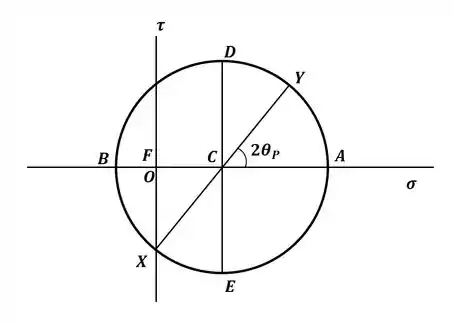
Então, com esses pontos, temos o seguinte círculo de Mohr:
Passo 3
Com o círculo de Mohr esboçado, vamos começar encontrando seu raio, que pode ser dado por:
Substituindo os valores conhecidos, teremos:
Agora vamos encontrar a inclinação dos planos principais , então teremos:
Substituindo os valores conhecidos, chegamos em:
Passo 4
Agora, para a letra (a), vamos rotacionar o elemento diferencial 25° no sentido horário, o que implica em uma rotação de 50° no sentido horário no círculo de Mohr, dessa forma, os novos pontos X’ e Y’ serão:
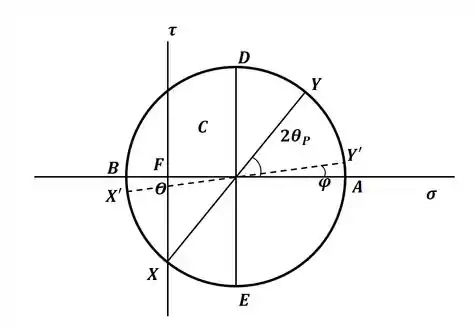
Com isso, podemos encontrar o ângulo formado, que será:
Sendo assim, a tensão normal na direção x pode ser encontrada através de:
Agora, para a tensão normal na direção y, teremos:
E, por fim, o cisalhamento pode ser encontrado através de:
Beleza! A letra (a) acabou aqui! Agora falta a letra (b) só.
Passo 5
Agora, para a letra (b), vamos rotacionar o elemento diferencial 10° no sentido anti-horário, o que implica em uma rotação de 20° no sentido anti-horário no círculo de Mohr, dessa forma, os novos pontos X’ e Y’ serão:
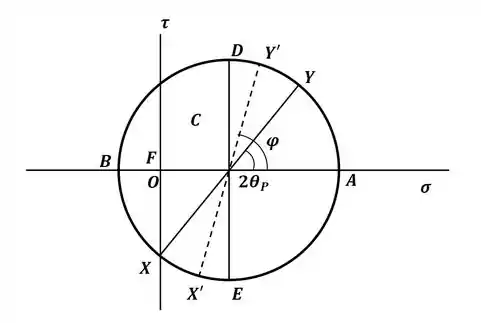
Com isso, podemos encontrar o ângulo formado, que será:
Sendo assim, a tensão normal na direção x pode ser encontrada através de:
Agora, para a tensão normal na direção y, teremos:
E, por fim, o cisalhamento pode ser encontrado através de:
Prooonto! Agora terminamos de vez!