Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas de Revisão - Ex. 123
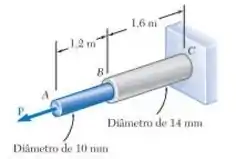
A haste é feita de aço para o qual a tensão de escoamento é e ; a haste é feita de uma liga de alumínio para a qual e . Determine a máxima energia de deformação que pode ser absorvida pela haste composta sem que ocorram deformações permanentes.
Passo 1
Fala aí, galera. Beleza? Vamos praticar mais mecânica pra tirar aquele na prova.
Para determinarmos a máxima energia de deformação que pode ser absorvida pela haste composta sem que ocorram deformações permanentes, temos que primeiro calcular a área das duas hastes:
Para a haste , temos que a área da seção transversal do cilindro é dada por:
Substituindo:
E para a haste , temos:
Passo 2
Em seguida, vamos utilizar a relação da tensão de escoamento. Ela é dada pela razão da carga aplicada pela área da seção. Portanto:
Neste caso, temos que usar a tensão de escoamento em para cada haste. Então, vamos encontrar a carga total para cada uma das hastes. Como a haste é composta por aço, temos:
E para , composta por alumínio, temos:
Opa, encontramos as duas cargas. Agora bora calcular a máxima deformação
Passo 3
Por fim, vamos lembrar que a a energia de deformação é uma grandeza escalar, portanto, a máxima energia de deformação vai ser a soma das energias de deformação para cada haste. Fica assim:
E então basta substuirmos valores. Para a carga, vamos utilizar a menor carga que encontramos no passo anterior, logo:
É isso, galera Bora pra próxima?