Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 109
Para a barra composta do , determinar a tensão residual em cada porção da barra, se cresce gradualmente desde zero até a deflexão do ponto C atingir um valor máximo e então decresce até zero, quando:
Passo 1
O enunciado nós da os seguintes dados sobre o nosso problema
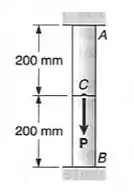
E queremos saber quanto é a tensão residual em cada um dos itens. Como sabemos a deformação que está sendo imposta, podemos verificar quanto é a tensão que ela causa. Com isso sabemos que a tensão que ela causa é:
Então sabemos que a tensão máxima que age é a tensão de , e olhando as tensões admissíveis temos que:
Como a tensão que age é maior que a tensão admissível, para termos a tensão residual, basta fazermos a diferença entre as tensões, com isso teremos que a tensão residual da barra AC será:
Já para o trecho BC, teremos que:
E como a tensão que age é menor que a admissível, não teremos deformações plásticas, e se não temos deformações plásticas, não temos tensões residuais no trecho BC.
Então sabemos que a tensão máxima que age é a tensão de , e olhando as tensões admissíveis temos que:
Como a tensão que age é maior que a tensão admissível, para termos a tensão residual, basta fazermos a diferença entre as tensões, com isso teremos que a tensão residual da barra AC será:
Já para o trecho BC, teremos que:
Como a tensão que age é maior que a tensão admissível, para termos a tensão residual, basta fazermos a diferença entre as tensões, com isso teremos que a tensão residual da barra BC será: (OBS: tem que se lembrar que como o trecho BC está sendo comprimido, devemos usar as tensões com valor negativo)