Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 67

Torques de mesma intensidade T são aplicados aos eixos de aço AB e CD. Utilizando o método do trabalho e energia, determine o comprimento L da porção vazada do eixo CD para que o ângulo de giro em C seja igual a 1,25 vezes o ângulo de giro em A.

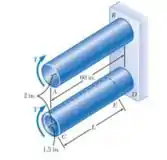
Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

T é o mesmo para cada eixo.

θ C = 1,25 θ A         U A B = 1 2 T θ A       e         U C D = 1 2 T θ C

Portanto U C D = 1,25   U A B

Eixo AB:

L A B = 60 i n .       c = 2 i n         J A B = π 2 c 4 = π 2 ( 2 ) 4 = 25,133   i n 4

U A B = T 2 L A B 2 G J A B = T 2 60 2 G 25,133 = 2,3873 T 2 2 G

Porção CE do eixo:

L C E = L ,         c o = 2 i n . ,           c i = 1,5 i n .

J C E = π 2   c 0 4 - c 0 4 = π 2 2 4 - 1,5 4 = 17,1806   i n 4

U C E = T 2 L C E 2 G J C E = T 2 L 2   17,1806 = 0.058205 T 2 L 2 G

Passo 2

Porção do eixo ED:

L E D = 60 - L ,           J D E = J A B = 25,133   i n 4

U E D = T 2 L E D 2 G J E D = T 2 60 - L 2 G 25,138 = 2,3873 T 2 2 G - 0,03978 T 2 L 2 G  

Eixo CD:

U C E + U E D = 2,3873 T 2 2 G + 0,018416 T 2 L 2 G J

Usando Eq: (1), 2,3873 T 2 2 G + 0,018416 T 2 L 2 G = 1,25 2,3873 T 2 2 G  

0,018416 L = 0,25 2,3873 = L = 32,4   i n .

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de L = 32,4   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada elemento da treliça é mostrada é feito de aço e tem uma área de seção transversal conforme apontado. Usando E = 29 × 10 6p s i , determine a energia de deformação .
O anel D é liberado do repouso na posição mostrada, e o seu movimento é interrompido por uma pequena placa fixada à extremidade C da barra vertical A B C . Determine a massa do anel para o qual a tens
Dois eixos sólidos de aço são conectados pelas engrenagens mostradas. Utilizando o método do trabalho e energia, determine o ângulo de rotação que descreve a extremidade em D quando T = 820N ∙ m . Uti
Para a viga prismática mostrada, determine a inclinação no ponto D .
A barra de aço A B C tem seção transversal quadrada com 19,05m m de lado e é submetida a uma carga P de 222,4k N .Usando E = 200G P a , determine a flexão no ponto C .