Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 12
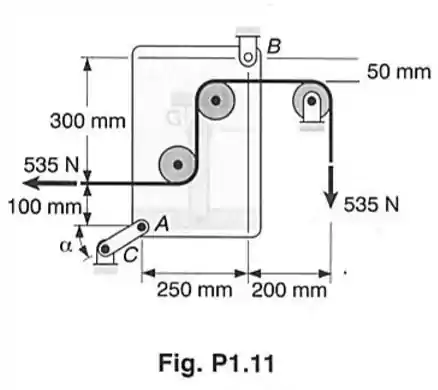
A haste de ligação AC do problema 1.11 tem uma seção transversal retangular uniforme de 3,2 mm de espessura e 25,4 mm de largura. Determine a tensão normal na porção central da haste, quando .
Passo 1
O problema pede a tensão normal na haste AC, para achar a tensão normal precisamos da força atuante na haste AC, assim como a sua área.
A área pode ser facilmente calculada com as dimensões da seção transversal (que é um retângulo de .
Já a força nós vamos ter que fazer o desenho do corpo livre e analisar as forças atuantes. No desenho não fica muito explícito mas as duas polias estão fixadas na placa que contém os pontos A e B.
Então vamos lá!
Passo 2
Primeiro vamos calcular a área:
Pronto! Nesse caso é só isso, porque o problema pediu a tensão na parte CENTRAL da barra!
Passo 3
Agora vamos achar a força, para isso vamos desenhar o corpo livre, lembrando que neste caso , logo a força atuante em A é horizontal:
Como queremos achar , que é a força que atua na barra AC, basta calcularmos o momento em relação ao ponto B (que deve ser igual a zero, porque o corpo está estático).
As forças de reação em B naõ produzem momento, e considerando o sentido horário o positivo vamos ter:
Passo 4
Agora basta substituir na equação da tensão normal: