Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 15

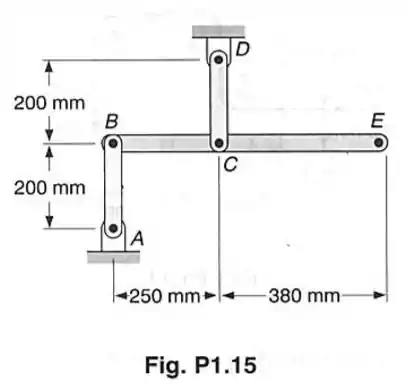
Cada uma das hastes de ligação AB e CD tem uma seção transversal retangular uniforme de e está ligada à barra horizontal BCE por pinos de diâmetro igual a . Considerando que a tensão normal média de ambas hastes não exceda a 170 MPa, determine a máxima carga que pode ser aplicada no ponto E, se esta carga é dirigida (a) verticalmente para baixo; (b) verticalmente para cima.

Passo 1

Neste problema vamos ter que achar as forças atuantes nas hastes AB e CD e, com a área transversal dessas hastes, achar a tensão normal.

O problema também deu o diâmetro dos pinos de forma a a podermos calcular a área da haste menos a área correspondente ao furo do pino. Porém, uma haste de de largura e de espessura não comporta um pino de de diâmetro, então vamos ignorar o pino e calcular a tensão normal na seção média das hastes.

Passo 2

Vamos achar as forças atuantes nas hastes fazendo o diagrama de corpo livre da barra BCE:

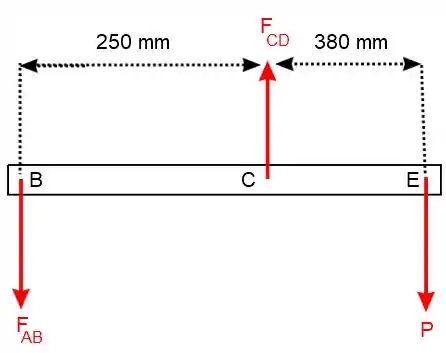
Agora vamos ter que aplicar o somatório de momentos e o somatório das forças em para achar as forças e :

Considerando o sentido horário positivo:

Considerando o eixo positivo para cima:

Logo o fator limitante, ou seja, a haste que está suportando uma maior força (e consequentemente tensão) será a haste CD.

Passo 3

Para que a tensão não exceda nem nenhuma haste vamos ter que considerar a haste CD (porque o carregamento nela é maior) e aplicar a equação da tensão normal.

Onde a força é igual a e a área é a do retângulo de .

Como a tensão máxima é de

Passo 4

Para a letra b as contas não vão mudar em nada, apenas os sentidos de todas as forças serão invertidos (em 180°) e, com isso, as tensões de tração se transformarão em tensões de compressão.

Porém o módulo de nenhuma força se alterará, portanto, o valor de será o mesmo.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a barra composta do Prob 2.9, determinar a maior carga P admissível se a deformação total da barra não deve exceder a 1mm e a tensão normal ser no máximo igual a 180 Mpa

Para a barra composta do Prob 2.10, determinar a maior carga P admissível se em valores absolutos a deformação total da barra e sua máxima tensão normal não podem exceder a 0,2 m m e 75 M P a , respec

Expressando por ε a “deformação técnica” em uma amostra tracionada, mostre que a determinação exata é ε t = ln ⁡ 1 + ε .

O volume de uma amostra tracionada é essencialmente constante, enquanto a derformação plástica ocorre. Se o diâmetro inicial da amostra é d 1 , mostre que quando o diâmetro é d 2 a deformação é ε t =

Determinar a deflexão do cume A de um paraboloide de revolução homogêneo, de altura h , densidade ρ e módulo de elasticidade E , devido ao seu próprio peso.