Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 57
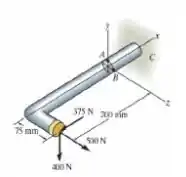
A haste maciça de 25 mm de diâmetro está sujeita às cargas mostradas na figura. Determine o estado de tensão no ponto B e mostre os resultados em um elemento diferencial localizado nesse ponto
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você??
Bom, nosso enunciado nos diz que esse painel recebe uma carga uniforme na sua superfície, e nos pede o estado de tensão nos pontos A e B da seção transversal.
Isso é uma questão típica de esforços combinados. Tem um passo a passo para resolver. Vem que tem mostro!
Passo 2
Nosso primeiro passo será calcular nossas forças internas, ou seja, a normal, os momentos e os cortantes na nossa seção. Para as forças no eixo :
Agora as forças no eixo :
E também para o eixo :
Do mesmo modo, podemos obter os momentos em cada eixo, primeiro no eixo vamos ter que:
No eixo :
E por fim no eixo :
Passo 3
Agora, vamos pescar outros dados que são beeeeem importantes pra gente. As características geométricas da nossa seção.
A distância do nosso ponto até o centro da seção é:
O valor do momento estático do segmento que passa pelo ponto vai ser o produto entre o centroide de um semicírculo e a área do semicírculo, que dá:
Momento de inércia:
Momento polar de inércia:
E a coordenada do ponto em é:
Passo 4
Agora que já temos todo o necessário para calcular nossas tensões, por que vamos esperar?? Só bora comigo.
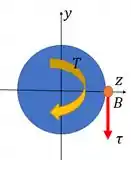
Nosso ponto vai sofrer tensão normal (tração) por causa do esforço normal. E vai sofrer compressão por causa do momento . O momento não vai gerar tensão porque está na linha neutra.
O cortante em não vai gerar cisalhamento em , porque está na parte superior da seção em relação a esse esforço. Mas ele sofre cisalhamento por causa da torção e de .
Repara que esses cisalhamentos estão na mesma direção, por isso que pudemos soma-los. O cisalhamento da torção também acompanha o sentido do momento torçor quando passa por ele.
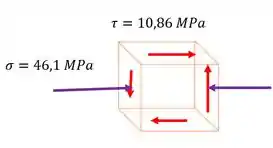
Aí nosso elemento fica:
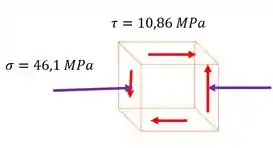
Resposta
