Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 31
Duas forças de são aplicadas a um elemento de máquina AB em forma de L, conforme mostrada a figura. Determine as tensões normal e de cisalhamentos (a) no ponto a ,(b)no ponto b ,(c)no ponto c.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede para a gente determinar as tensões normal e de cisalhamentos (a) no ponto a ,(b)no ponto b ,(c)no ponto c.
Seja o ângulo de inclinação da linha AB.
Desenhe um esboço de corpo livre da parte do elemento de máquina que fica acima da seção abc.
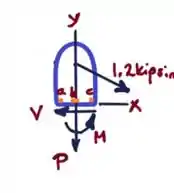
Passo 2
Considere os esforços e o momento para determinarmos ;)
Propriedades da seção:
- Ponto a:
(b) Ponto b:
(c) ponto c
Resposta
Exercícios de Livros Relacionados
Uma barra de seção transversal quadrada de 30 mm por 30 mm tem 2 m de comprimento e é segura pela mão por uma das extremidades, com a outra volta para cima. Se tiver massa de 5 kg/m, determine o maior
O cilindro de peso desprezível repousa sobre um piso liso. Determine a distância excêntrica e y na qual a carga pode ser posicionada de modo que a tensão normal no ponto A seja nula.
Resolva o Problema 8.26 para o ponto B .
Visto que o concreto só pode suportar pouca ou nenhuma tração, esse problema pode ser evitado se o concreto for protendido com cabos ou hastes. Considere a viga simplesmente apoiada mostrada na figura
A pilastra de alvenaria está sujeita à carga de 800kN . Determine a equação da reta y=f ( x ) ao longo da qual a carga pode ser posicionada sem provocar tensão de tração na pilastra. Despreze o peso d